|
|
| Let's
set up the missing
cornerstone! |
|
| A
revealing insight into the polynomial function |
| Every
polynomial function has its initial position at the origin of the
coordinate system |
| There
are three methods to transform an n-th
degree polynomial written in the general form, |
| f
(x)
= anxn
+ an
-
1
xn
-
1
+ an
-
2
xn
-
2
+
. . . +
a2x2
+
a1x + a0 |
| to
its source form |
|
fs(x)
= anxn
+ an
-
2
xn
-
2
+ an
-
3
xn
-
3
+
. . . +
a3x3
+
a2x2
+ a1x, |
| whose
graph passes through the origin. |
| Each
method is based on the fact that a polynomial written in
general form represents translation of its source
(original) function in the direction of the
coordinate axes, where the coordinates of translations
are |
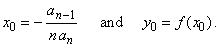 |
| Therefore,
each polynomial missing second term (an
-
1
=
0),
represents a source polynomial function whose graph is
translated in the direction of the y-axis
by
y0
= a0. |
| Let's
reveal all three methods. |
|
| First
method |
| If
we plug the coordinates of translations x0
and y0
with changed
signs into a given polynomial y
=
f
(x), expressed in the general form,
i.e., |
| y
+ y0
= an(x
+ x0)n
+ an
-
1(x
+ x0)n
-
1
+
. . . +
a1(x
+ x0)
+ a0 |
| then,
after expanding and reducing the above expression we get
its source function fs(x). |
| Inversely,
by plugging the coordinates of translations into the
source polynomial function, i.e.,
|
|
y
- y0
= an(x
- x0)n
+ an
-
2(x
- x0)n
-
2
+
. . . +
a2(x
- x0)2
+ a1(x
- x0), |
| after
expanding and reducing the above expression, we get given polynomial
f (x). |
| Note
that the complete source polynomial has n
-
1 terms, missing
second and the absolute term. |
|
| Second
method |
| The
coefficients a,
of the source polynomial function are related to
corresponding value of the derivative of the given polynomial at x0,
like coefficients
of the Taylor polynomial in Taylor's or Maclaurin's formula,
thus |
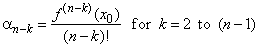 |
| where,
an
= an,
an
-
1
= 0,
a0
= f
(x0),
and f
(n
-
k)(x0)
denotes the (n
- k)-th
derivative at x0. |
| Observe
that
coefficients of the source polynomial function define the value and
the direction of the vertical translation of successive derivatives of given
polynomial that is, |
| f
(n
-
k)(x0)
= (n
- k)! an
-
k . |
| Further,
the horizontal translation of each successive derivative
corresponds with x0
of the given
polynomial function. |
| For
example, the coefficient a1
of the source cubic function
f (x) =
a3x3
+
a2x2
+
a1x + a0 |
| since
f ' (x)
=
3a3x2
+ 2a2x
+
a1
and x0
=
-
a2/(3a3)
then |
 |
| Thus,
fs(x) =
a3x3
+ a1x
is the source cubic polynomial function, |
| where
the coefficient a1
equals the slope of the tangent line at the inflection
point I (x0,
y0). |
| Further,
as a1
=
f ' (x0),
the coefficient a1
also represents the vertical translation of the first
derivative of the cubic polynomial, that is why the sign
of the product a3a1
is used as the additional condition in the classification
of the cubic polynomial shown later. |
|
|
|
|
|
|
New:
1.
Trigonometry
1 Applications of Trigonometry:
|
|
- the book is now available in paperback on the Amazonís book store, Please visit,:
|
|
https://www.amazon.com/Trigonometry-1-Applications-Vladimir-Serdarushich/dp/1535303905
|
|
2.
Vectors
and Coordinate Geometry:
|
|
- the book is now available in paperback on the Amazonís book store, Please visit,:
|
|
http://www.amazon.com/Vectors-Coordinate-Geometry-Vladimir-Serdarushich/dp/1523688661
|
|
3.
Analytic Geometry:
the book is now available in paperback on the Amazonís book store:
|
|
Please visit, http://www.amazon.com/Analytic-Geometry-Vladimir-Serdarushich/dp/1514653435
|
| *
For additional information the author invites an
interested visitor to visit the Register
page. |
| Observe
that the content of the website is exclusively intended
for personal use and is copyright protected. |
|
| Author:
Vladimir Serdarushich |
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|

| Registered
with the IP Rights Office
Copyright Registration Service
Ref: 413180394 |
|
|
|
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
|
|