|
| A
revealing insight into the polynomial function -
continue |
|
|
|
|
|
|
|
| Third
method |
| Sigma
notation of the polynomial, where the coefficients a
of
the source polynomial are represented by a recursive formula. |
| Finally,
the polynomial |
| f
(x)
= y = anxn
+ an
-
1
xn
-
1
+ an
-
2
xn
-
2
+
. . . +
a2x2
+
a1x + a0
we can write |
|
|
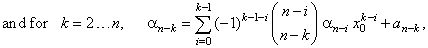 |
|
while, for k
= 0,
an
=
an, |
|
|
|
and from an-
k,
for k
=
n,
a0
=
f
(x0)
= y0. |
|
| Thus,
the expanded form of the above sum is |
| y
- y0
= an(x
- x0)n
+ an
-
2(x
- x0)n
-
2
+
. . . +
a2(x
- x0)2
+ a1(x
- x0) |
| where
x0
and y0
are coordinates of translations
of the graph of the source polynomial |
| fs(x)
= anxn
+ an
-
2
xn
-
2
+
. . . +
a2x2
+ a1x
|
| in the direction of
the coordinate axes. |
|
| Use of the
properties of the polynomial |
| Therefore, we can
write linear function
or the
polynomial of the first degree |
| f
(x)
= y = a1x
+ a0
or y
= a1(x
-
x0)
or y
-
y0
= a1x, |
| where
|
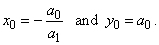 |
|
|
| By setting x0
= 0 or y0
= 0
we get y
= a1x
the source linear function. |
|
| Polynomial of
the
second degree or quadratic function |
|
f (x) =
a2x2
+ a1x
+ a0
or y
-
y0
= a2(x
-
x0)2, |
| where
|
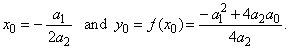 |
The
turning point T
(x0,
y0). |
|
| If x0
= 0 and y0
= 0 then, y
= a2x2
is the source quadratic. |
|
| Polynomial of
the
third degree or cubic function |
|
f (x) =
a3x3
+
a2x2
+ a1x
+ a0
or y
-
y0
= a3(x
-
x0)3
+
a1(x
-
x0) |
| where
|
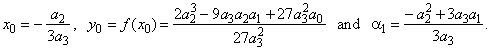 |
|
|
| By
setting x0
=
0 and
y0
= 0 we get
the source cubic function |
|
y
=
a3x3
+
a1x
where a1=
tan at |
|
therefore,
the coefficient a1
shows the slope of the tangent line at the point of inflection
I (x0,
y0). |
|
| Polynomial of
the fourth degree or quartic |
|
f (x) = a4x4
+
a3x3
+
a2x2
+ a1x
+ a0
or y
-
y0
= a4(x
-
x0)4
+
a2(x
-
x0)2
+
a1(x
-
x0) |
| where,
|
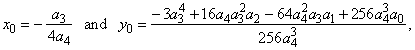 |
|
|
|
|
| By
setting x0
=
0 and
y0
= 0 we get |
|
y
=
a4x4
+
a2x2
+
a1x,
the source quartic function. |
| Thus, we can proceed
with, quintic, sextic or an nth
degree polynomial. |
|
|
|
|
|
|
| *
For additional information the author invites an interested
visitor to visit the Register
page. |
|
|
|
|
|
|
|
|
|
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |