|
| A
revealing insight into the polynomial function -
continue |
|
|
|
|
|
|
|
| Benefits the
principle provide |
| Let's show
here only a few of the benefits the principle brings. |
| Classification
of the polynomial functions |
| The first, the
principle enables classification of the polynomial functions meaning, it
provides basic conditions for particular type of function, or
group of functions, an nth
degree polynomial includes. |
| That is, defines the
form of the graph specific type of a polynomial function is represented. |
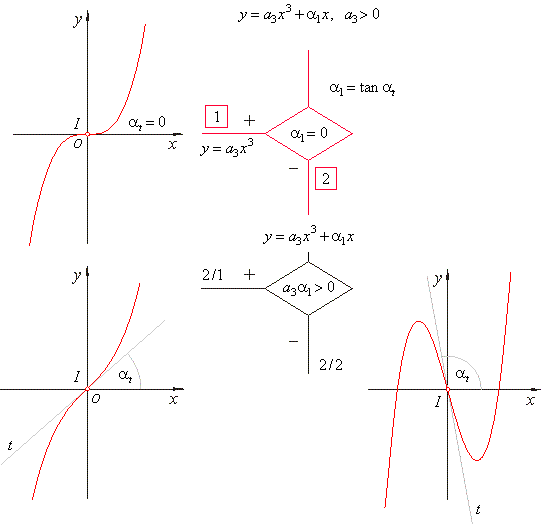
| Thus for example,
cubic polynomial consists of three types, or is represented by
three distinct forms (shapes) of graphs of functions. |
 |
| Using the same
approach classified is the quartic polynomial to ten types of
characteristic functions and so on. |
| Each nth
degree polynomial is classified using the same basic criteria
that include, examination of appearance or exception of each
of the source coefficients a,
and depending on the sign of their product with the leading coefficient an,
since the source
coefficients show the direction of the vertical
translation of the corresponding derivative. |
| The
classification also defines all variations of a polynomial
expression related to the changes of polarity of
the variables such
as, f (-x),
-
f (x)
and -
f (-x)
that
cause the reflections of the graph of the polynomial function
around the y-axis, x-axis
and both axes, respectively. |
| Observe that the
first criteria of the classification separates even and odd nth
degree polynomials called the power functions or monomials as the first
type, since all coefficients a
of their source function vanished, (see the above diagram). |
|
| Therefore, we
write the
translated
power (or monomial) function
or the first type |
| y
- y0
= an(x
- x0)n, |
| where x0
= -
an
-
1/(nan),
y0
=
f
(x0)
and n
is an even or
an odd positive integer.
|
| For
n
= 2m, m Î
N the even
power function has, |
|
the
turning point T
(x0,
y0) |
|
and
the real roots if an
y0
<
0, |
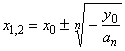 |
| as
shows the right figure (where an
> 0 ). |
|
 |
|
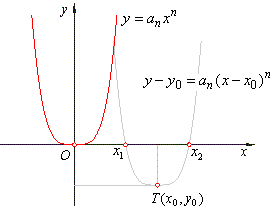
| For
n
= 2m + 1, m Î
N the odd power function |
|
has,
the point of inflection I
(x0,
y0),
at
=
0 |
|
and
the root |
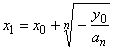 |
| as
shows the right figure (where an
> 0). |
|
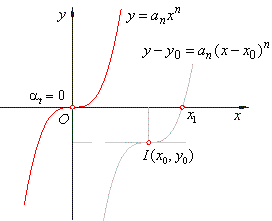 |
|
|
|
|
|
|
|
| *
For additional information the author invites an interested
visitor to visit the Register
page. |
|
|
|
|
|
|
|
|
|
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |