|
| The
determinant of a matrix |
| Determinants
are defined only for square matrices. |
| The
determinant D
of an n-by-n
matrix A,
also denoted det(A)
or |A|
is an ordered square array of elements |
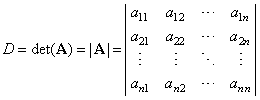 |
| the
value of which is given by an alternating sum of products of the
elements of A,
that can be obtained |
| by
using the method of expanding the determinant to
cofactors. |
|
|
Expanding a determinant
by cofactors
|
| That
is, the value of a determinant equals the sum of the products of
the entries in anyone row or column and their
respective cofactors. |
| A cofactor
of an entry aik
is
a signed minor or (a sub-determinant) derived from a given matrix or
determinant
by the deletion of the row and column containing the specified
entry. |
| Therefore, the
cofactor
of the entry aik
of a matrix A |
| Aik =
(-1)i
+ k · Dik
, |
| where
Dik
is the minor (or subdeterminant) of the matrix A
obtained by deleting its ith
row and kth
column. |
| A
determinant can be expanded along any row or column without
affecting the determinant's value. |
| Thus,
the value of a determinant of order n
expanded along the kth
column |
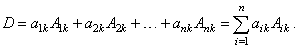 |
| where
k
can be any column between 1 and n. |
|
| Calculating the value
of a determinant |
| The
determinant of a 2-by-2
matrix |
| Let
apply the above formula to calculate the value of the
determinant of a 2
´
2
matrix A, |
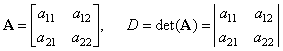 |
| then,
the expansion of the above determinant by the first column |
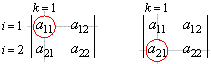 |
| thus,
obtained is |
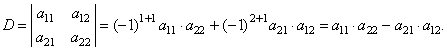 |
|
| The
determinant of a 3-by-3
matrix |
| Using
the above determinant expansion by cofactors formula we calculate the value of the
determinant of a 3
´
3
matrix A, |
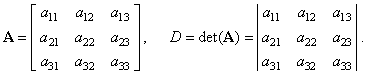 |
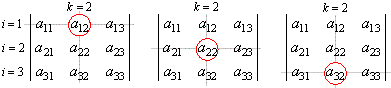
| The
diagram below shows the method of determining cofactors of the 2nd
column's entries, as we chose to expand
the above determinant along that column |
 |
| thus,
obtained is |
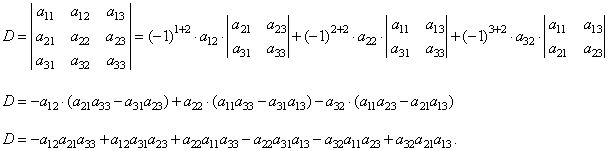 |
|
| Example:
For the given 3-by-3
matrix
A, find the
value of the determinant D
= det(A),
|
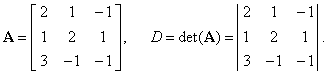 |
| By
expanding the determinant by the first column obtained is |
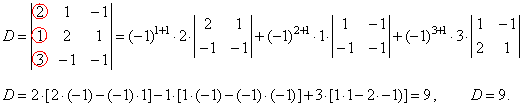 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Matrices, determinants and systems of linear equations
contents
|
|
 |
|
|
|
Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved.
|