|
| The
determinant of a matrix |
| Determinants
are defined only for square matrices. |
| The
determinant D
of an n
´
n
matrix A,
also denoted det(A)
or |A|
is an ordered square array of elements |
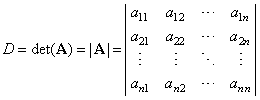 |
| the
value of which is given by an alternating sum of products of the
elements of A,
that can be obtained by
using the method of expanding the determinant to
cofactors. |
|
| Properties of determinants |
| Use of the following properties simplify calculation of the value of
higher order determinants. |
| 1.
Interchanging (switching) two rows or columns changes the sign
of the determinant. |
| 2.
A determinant with a row or column of zeros has value 0. |
| 3.
A determinant with two rows or columns equal (or proportional) has value 0. |
| 4.
A common factor of all elements of a row or a column can be factored out. |
| 5.
The multiplication of a determinant by a scalar can be done by multiplying each element of any row or column by the scalar. |
| 6.
The determinant of a triangular matrix is equal to the product
of the diagonal elements. |
| 7.
The value of a determinant will not change by adding multiples of
any column or row to any other column or row. |
| 8.
A
determinant can be expanded along any row or column (without
affecting the determinant's value). |
|
| Therefore,
we use the above properties to set as many zeros in a row or column as possible to simplify calculation of the value of
a determinant. |
| Example:
Let find the
value of the determinant of the matrix A
from the previous example applying the method of expanding the determinant to
cofactors and using properties of determinants.
|
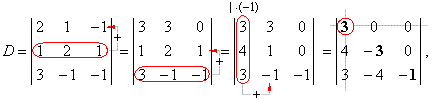 |
| First,
added is the second row to the first writing the sum to the
first row. Then we add third row to second, writing
the sum to the second row. Finally, the first column multiplied
by -1
we added to the second column to
obtain the triangular matrix. |
| By
expanding the above triangular matrix by the first column
obtained is |
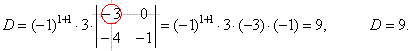 |
| This
way proved is the 6th
property stating that the determinant of a triangular matrix is
equal to the product of
its diagonal elements. |
|
| The
inverse of a matrix |
| The
inverse matrix A-1,
of a square matrix A,
is the matrix which when multiplied by A
on either side gives the
identity matrix I
(the
identity matrix is a square matrix in which every main diagonal
entry is 1 and the other
elements are all
zero), |
| AA-1 =
A-1A =
I . |
| The
inverse of a regular square matrix A = [aik]
(with a non zero determinant) we obtain dividing each entry of the transpose of the cofactor
matrix of A, called the adjoint matrix,
by the value of determinant of A,
i.e., |
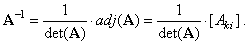 |
| The
entries of the cofactor matrix [Aik] |
| Aik =
(-1)i
+ k · Dik
, |
| where
Dik
is the minor (or subdeterminant) of the matrix A
obtained by deleting its ith
row and kth
column. |
| Interchange the rows and columns
of the cofactor matrix to
obtain [Aki]
the transpose of the cofactor matrix. |
|
| Example:
Find the inverse of the 3
´
3 matrix A
from the previous example.
|
| Solution:
By
expanding the det(A)
by the second row obtained is,
|
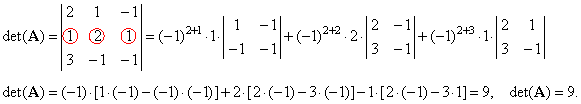 |
| Then
calculate the cofactors Aik, |
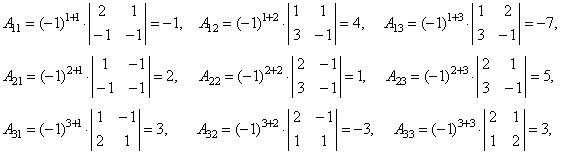 |
| to
write the cofactor matrix [Aik] |
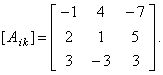 |
| By
flipping the cofactor matrix [Aik]
around the main diagonal
obtained is the adjoint
matrix [Aki]
or the transpose
of the cofactor matrix. |
| Therefore, the inverse of the
matrix A |
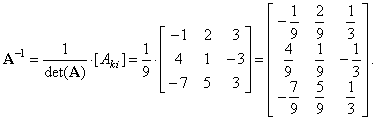 |
| Let
verify that the matrix A
multiplied by its inverse gives the identity matrix, |
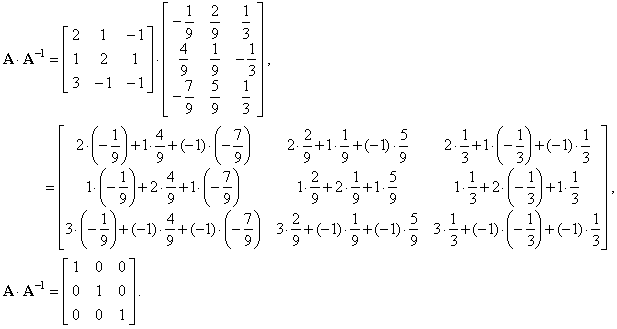 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Matrices, determinants and systems of linear equations
contents
|
|
 |
|
|
|
Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved.
|