| A
lower triangular matrix is a square
matrix in which all elements above the main diagonal are zeros. |
| Square
matrices for which aij
= aji
are called symmetric about the main
diagonal. |
| Examples
of square matrices |
| |
The
diagonal matrix of order 4, |
|
The
identity matrix of order 3, |
|
| |
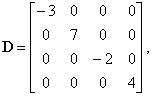 |
|
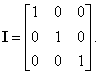 |
|
|
| |
The
upper triangular matrix of order 4, |
|
The
lower triangular matrix of order 4, |
|
| |
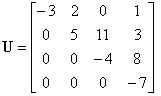 |
|
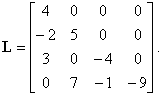 |
|
|
|
The
symmetric matrix of order 5, |
|
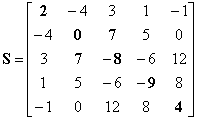 |
The
elements of the main diagonal are in bold. |
|
| A
matrix whose all elements are zero is called the null
matrix, written 0. |
|
| Vectors |
| A
matrix with only one row or one column is called a vector. |
| A
matrix with one row and n
columns is called a row vector. |
| A
matrix with one column and m
rows is called a column vector. |
|
| Transposition |
| The
transpose is the matrix derived from a given matrix by
interchanging the rows and columns. Thus, the
transpose of a matrix A
of order
m
´
n
is another matrix
denoted AT
of order n
´
m. |
| Therefore,
to transpose means to interchange the rows and columns of a
matrix, that
is, |
| AT
= [aji],
where j
is the column and i
is the row of matrix A
= [aij]. |
| Example:
Given a matrix A
of order 3 ´
4, find the transpose AT.
|
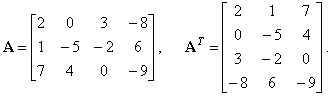 |
|
| Basic
matrix
operations |
| Matrix addition and
subtraction |
| Matrices
can be added or subtracted only if they have the same
dimensions. |
| Addition |
| The
elements of the sum of the two matrices with the same
dimensions, A
and B,
are equal to the sums of the
corresponding elements aij
+ bij
that is, |
| A
+ B
= [aij
+ bij]. |
| Subtraction |
| The
elements of the difference of the two matrices with the same
dimensions, A
and B,
are equal to the differences
of the corresponding elements aij
-
bij
that is, |
| A
-
B
= [aij
-
bij]. |
| Example:
Given are matrices, A
and B, find the
sum A
+ B
and the difference A
-
B.
|
| |
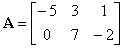 |
and |
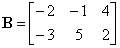 |
|
|
| |
then, |
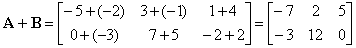 |
|
|
| |
and |
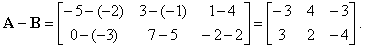 |
|
|
|
| Scalar
multiplication of a matrix |
| Multiplication
of a matrix A
by a scalar c
is defined as |
| c
· A = [c · aij], |
| that
is, each element of the matrix is multiplied by c.
Therefore, if c
= 0, the result is the null
matrix. |
| Example:
Given the matrix |
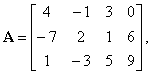 |
find the
product -
2 · A. |
|
|
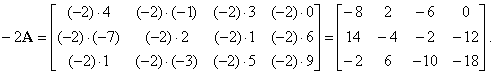 |
|
| Matrix
multiplication |
| Multiplication
of two matrices is defined only if the number of columns of the
first matrix equals the number of rows
of the second. Matrices that satisfy this condition are said to
be conformable. |
| If
A
= [aij]
is a matrix of order m
´
n
and B
= [bjk]
is a matrix of order n
´
p,
then the product |
| C
= AB |
| where
C
= [cik]
is the m
´
p
matrix of which the ikth
entries are defined by the formula |
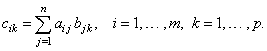 |
| Therefore, the
ikth
entry of the product equals the inner product of the components
of the ith
row of the first matrix
with the components of the kth
column of the
second matrix. |
| Example:
Given are conformable matrices, A
and B, find the
product AB.
|
| |
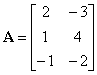 |
and |
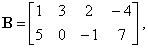 |
|
|
| then, |
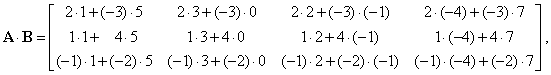 |
|
|
| or |
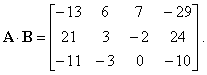 |
|
|
|
| The
matrix-vector product |
| If
A = [aij]
is an m
´
n
matrix, x =
{xj}
a column vector of order n,
and y = {yi}
a column vector of order m |
| then,
y = Ax
is the matrix-vector product, |
| where |
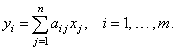 |
|
|
| The
column dimension of the matrix A
must equal the row dimension of the vector x
to obey the product definition. |
| Example:
Given is the matrix A
of order 2
´
3
and the column vector x
of order 3, find the
product Ax.
|
| |
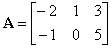 |
and |
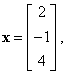 |
|
|
| then, |
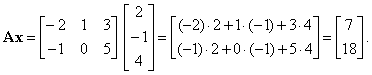 |
|
|
|
| If A is
a square matrix of order n
then,
|
| AI =
IA = A |
| where
I is the
identity
matrix of order n. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Matrices, determinants and systems of linear equations
contents
|
|
 |
|
|
|
Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved.
|