|
|
|
|
Series |
 Infinite series
Infinite series |
|
Convergence
of infinite series |
|
Divergence
of infinite series |
|
Convergent
and divergent series
examples |
 Harmonic
series
Harmonic
series |
|
|
|
|
|
|
| Convergence
of infinite series |
| If
the
limit of the sequence of partial sums
exists
as a real number, then the series is convergent. |
|
| Divergence
of infinite series |
| If
the limit of the sequence of partial sums does not exist or tends to
+
oo
or -
oo, |
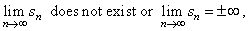 |
| then,
the series is divergent or oscillates. |
|
| Convergent
and divergent series
examples |
| Example: Show
that the series |
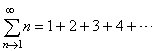 |
diverges. |
|
| Solution:
The given
infinite sum of natural numbers is called the arithmetic series. |
| Using
the formula for the sum
of the arithmetic sequence, whose difference d
= 1,
we calculate the sum of the first n
terms of the series. |
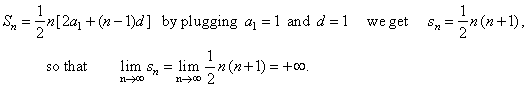 |
|
| Example: Let
show
that the series |
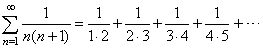 |
converges. |
|
| Solution:
We
use the method of partial
fraction decomposition to rearrange given expression. |
| Since
the denominator consists of linear factors then, we can write |
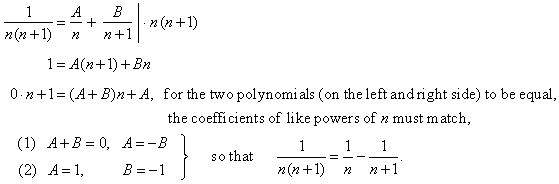 |
| Therefore, |
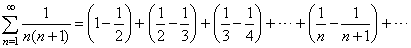 |
|
| Since
the second and the first term of any two successive parentheses cancel
then,
the sum of
the first n
terms of the series |
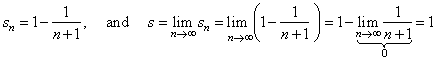 |
|
therefore the series converge, and its sum s
= 1. |
|
| Example: Show
that the series |
 |
converges. |
|
| Solution:
Use the method of partial
fraction decomposition to rearrange given expression. |
| Since
the
number of the coefficients used in the expansion relates to the degree
of the polynomial in the denominator,
and as it consists of linear factors some of which are repeated
then, |
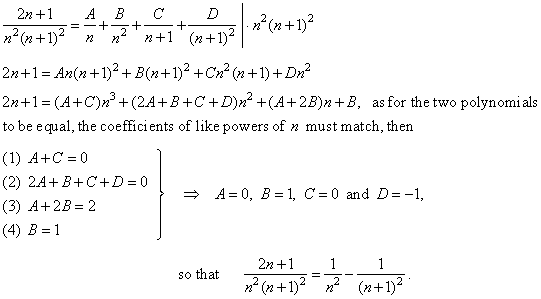 |
| Therefore, |
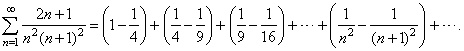 |
|
| Since
the second and the first term of any two successive parentheses cancel
then, the sum
of
the first n
terms of the series |
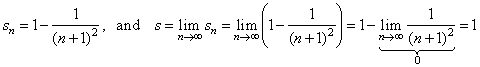 |
|
therefore the series converge, and its sum s
= 1. |
|
| Harmonic
series |
| The
series of the reciprocals of natural numbers |
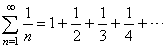 |
| is
called the harmonic series since the middle term of any three successive
terms is the harmonic mean of the
other two. |
| Given
three positive numbers, a,
b
and c
are said to be in the harmonic proportion if |
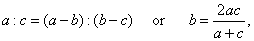 |
| that
is, if b
is the harmonic mean of the numbers, a
and c. |
| Therefore,
any three successive terms, |
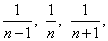 |
of
the harmonic series, are in the harmonic |
|
| proportion since |
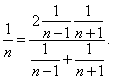 |
|
| As,
in the harmonic proportion a
> c then, a
-
b > b -
c therefore a
+ b > 3b -
c |
| or
a
+ b + c > 3b. |
| That
is, the sum of any three successive terms of the harmonic series is
three times greater than the middle term.
P. Mengoli (1626 - 1686) used this property to prove divergence of the
harmonic series. |
| Let
examine behavior of the sequence of partial sums of the harmonic series
applying this property. |
| Thus,
the sum of the three successive terms beginning from the second gives |
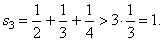 |
| Next
nine terms, from n = 5 to
13, divide in three groups with three terms in
each, so that; first gives |
|
|
| Therefore, |
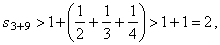 |
|
|
| since
the parentheses
equals already known value s3. |
| For
next 27
terms, from n =
14 to 40,
following the same procedure, we get that their sum is greater
than |
| |
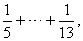 |
for
which is already shown that is >
1,
thus s3 +
9 + 27
> 3. |
|
|
| Generally,
it can be written |
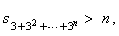 |
that
is, the partial sums sn increase
to infinity as n
®
oo. |
|
| Therefore,
the harmonic series diverges. |
|
|
|
|
|
|