|
|
Series |
 Infinite series
Infinite series |
|
The remainder
or tail
of the series |
|
Necessary
and sufficient
condition for the convergence of a series |
|
Necessary
condition for the convergence of a series |
|
The
n-th
term test for divergence |
 Properties
of series
Properties
of series |
|
The
product of two series or the Cauchy product |
|
|
|
|
|
|
|
| The remainder
or tail
of the series |
| As
with sequences, the convergence of an infinite series |
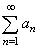 |
only
depends on the behavior of the |
|
| general
term of the series an
as n
increases to infinity, and not on any finite number of its initial
terms. |
| Note
that, since |
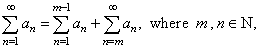 |
|
|
| the series |
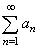 |
converges
if and only if |
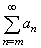 |
converges. |
|
| Therefore,
to show that a series |
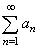 |
converges we can ignore any finite number of
terms |
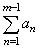 |
at the |
|
| beginning,
and just need to prove the convergence of the tail or remainder |
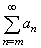 |
of
the series. |
|
|
| The
difference between the sum s
of a convergent series a1
+
a2
+ a3
+
. . . + an
+
. . .
and the nth
partial sum sn
is called the remainder (tail) rn
of the series, i.e., |
| rn
= s -
sn
= an + 1 + an + 2 +
an + 3 +
. . .
or
s = sn
+ rn. |
| Thus,
if a series |
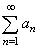 |
converges
then the remainder rn
= an + 1 + an + 2 +
an + 3 +
. . . converges
too, |
|
| that
is, since |
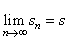 |
and
s
= sn
+ rn
then, |
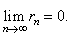 |
|
|
|
|
Necessary
and sufficient
condition for the convergence of a series - Cauchy's convergence test |
| Necessary
and sufficient
condition that the sequence of partial sums {sn}
of a given series converges, and |
| hence
the
series |
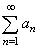 |
converges is,
that for given however small positive number e
it is possible find |
|
| an index n0 such
that |
sn
+ r -
sn
| < e
whenever
n
> n0(e)
and r =
1, 2, 3,
. . . , |
| or
expressed by terms of the series, if |
| |
an + 1 + an + 2 +
an + 3 +
. . . +
an + r
|
< e
whenever
n
> n0(e)
and r
= 1, 2, 3,
. . . . |
| Therefore,
a series converges if the absolute value of the sum of any finite number
of sequential terms can become
arbitrary small by starting the addition from a term which is far
enough. |
|
| Necessary
condition for the convergence of a series |
| Hence, it is necessary
condition for the convergence of a series that its terms tend to
zero as n
|
| increases to infinity,
that is |
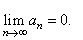 |
So,
if this condition is not satisfied the series diverges. |
|
| That
this condition is only necessary but not sufficient
condition for the convergence shows the harmonic
series for which |
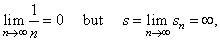 |
| as
was shown in previous section. |
| Necessary
condition for the convergence of a series is usually used to
show that a series does not converge. |
|
| The
nth
term test for divergence |
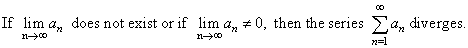 |
| Note
that this is only a test for divergence. That is, if we can prove that
the sequence {an}
does not converge
to 0,
then the infinite series does not converge. |
|
| Properties
of series |
| If
given are two convergent series, |
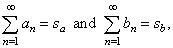 |
|
then the convergent series is obtained by adding or subtracting their
same index terms, and its sum equals the
sum or the difference of their individual sums, i.e., |
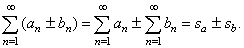 |
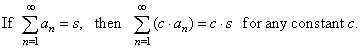 |
|
| The
product of two series or the Cauchy product |
| If
given are two convergent series of positive terms, |
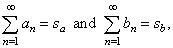 |
then the product |
|
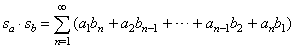 |
|
denotes the
convergent series sum of which is equal to the product of the sums of
the given series. |
|
|
|
|
|