|
| Series
|
|
Infinite series |
 Geometric
series
Geometric
series |
 P-series
P-series |
|
|
|
|
|
|
| Geometric
series |
| A
series, whose successive terms differ by a constant multiplier, is called a geometric series
and written as |
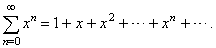 |
| If
| x | < 1 ;
the nth
partial sum is |
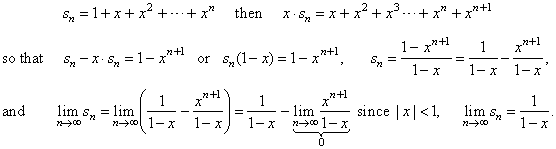 |
|
Thus, the geometric series is convergent if
| x | < 1
and its sum is |
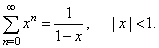 |
| If
| x | > 1
then the geometric series
diverges. |
|
| Example: Show
that the series |
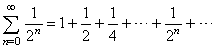 |
converges. |
|
| Solution:
Given
is the geometric series subsequent terms of which are multiplied by the
factor 1/2. |
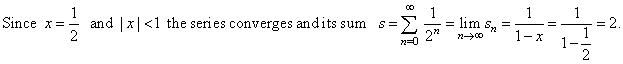 |
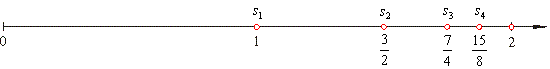 |
|
|
Example: Let
prove
that the pure recurring decimal 0.333
. . .
converges to 1/3.
|
| Solution:
Given
decimal can be written as |
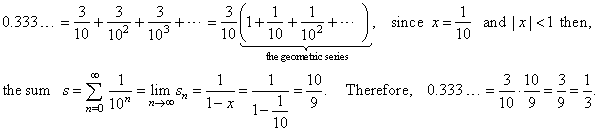 |
|
|
Example: Let
calculate the square of the convergent
geometric series
|
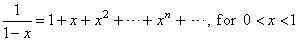 |
| using
the Cauchy product shown above. |
| Solution:
|
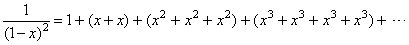 |
|
|
= 1 + 2x + 3x2
+ 4x3 + · · · + (n + 1)xn + · · · |
| the
obtained series |
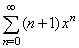 |
converges
for 0 < x
<1. |
|
|
|
| P-series |
| The
series |
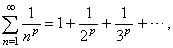 |
converges
if
fixed constant
p
> 1 and diverges if p
< 1. |
|
| By
grouping terms |
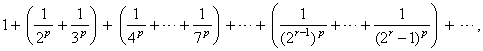 |
|
| where
the number of terms in parentheses form the sequence 2,
4, 8, ... 2r-1,
... such that |
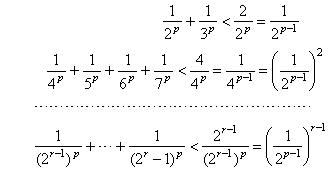 |
| therefore,
each value in parentheses is smaller than the corresponding term of the geometric
series |
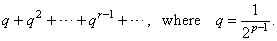 |
| Thus,
if p
> 1
then q
< 1,
the geometric series converges so that the given series is also
convergent. |
| Euler
discovered and revealed sums of the series for
p
=
2m,
so for example |
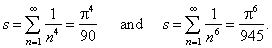 |
| If
p < 1
then np
< n or 1/np
> 1/n, therefore the
terms of the given series are not smaller than the terms of
the divergent harmonic series so, given series diverges. |
|
|
|
|
|