|
| Sets
and Relations |
|
|
|
|
|
|
Relations |
 The Cartesian product
The Cartesian product |
 The domain
and the range
The domain
and the range |
 Function
Function |
 Relation
on a set
Relation
on a set |
 Reflexive,
symmetric, transitive and equivalent relation
Reflexive,
symmetric, transitive and equivalent relation |
|
|
|
|
|
|
|
Relations |
| The
Cartesian product of two sets X and
Y, denoted
X
× Y, is
the set of all possible ordered pairs (x,
y)
where x is a
member of X
and y
is a member of Y: |
|
X ×
Y
= { (x,
y)
| x
Î
X
and y
Î
Y
} |
| A
relation R
from
X to
Y
is a subset of the
Cartesian product X
×
Y. The notations
(x,
y)
is an element of R
and x
R y
(x
is in relation to
y) are equivalent.
Formally, any set of ordered pairs which defines a relation
between the first member of each pair and its corresponding
second member. |
| |
| The
domain of a relation R
is the set of all the first
components of the ordered pairs that constitute the
relation.
The range of R
is the set of all the second components of
every ordered pair in
R.
|
| If each first member of a relation is associated with only one second member, the relation is a
function. |
|
| Example: |
Given is
set S
= {1, 3, 5, 7, 9} and relations on S: |
|
|
| R1 = {(1, 3), (3, 5), (5, 1), (3, 7), (7, 9), (9, 1)}, |
| R2 = {(1, 1), (3, 3), (5, 5), (7, 7), (9, 1)}, |
| R3 = {(1, 5), (3, 7), (7, 1), (9, 5), (1, 1)}, |
| R4 = {S
× S}. |
|
|
|
| Which of these relations is function from
S
to S ? |
| Solution:
A binary relation R, a subset of the Cartesian product A
×
B, is said to be a function from
A to
B if for
each x Î
A there is exactly one
y
Î
B, such that the pair
(x,
y) is in subset R. The set A is called the domain of the function, and the set
B is called the codomain of the function.
Thus, |
|
R2 = {(1, 1), (3, 3), (5, 5), (7, 7), (9, 1)} is the function from
S
to S. |
|
| Relation
on a Set |
| Let
X
be the given set, then a relation R
on X
is a subset of the Cartesian product of X
with itself, i.e., X
× X. |
| A
relation R
on X
is said to be reflexive if x
R
x
for every x
Î
X. |
| A
relation R
on X is
symmetric if x
R
y
implies that y
R
x. |
| A
relation R
on X is
transitive if x
R
y
and y
R
z imply
that x
R
z. |
| An
equivalence relation is relation on set X
that is reflexive, symmetric and transitive. |
|
| Example: |
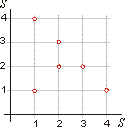
Supplement the relation
R
= {(1, 1), (2, 2), (3, 2), (4, 1)}, defined on the set
S
= {1, 2, 3, 4}, |
|
| with minimal number of elements of the product set
S
×
S
such that the relation becomes symmetric. |
| Solution:
The given relation should be supplemented with pairs (1, 4) and (2, 3). |
|
| The relation
R
= {(1, 1), (1, 4), (2, 2), (2, 3), (3, 2), (4, 1)} is symmetric (in
relation to the main diagonal). |
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
| Beginning
Algebra Contents |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
|
|