|
| Laws of the Algebra of Sets |
|
|
|
The
fundamental laws of the algebra of sets |
|
Sets and logic |
|
The
"and", the conjunction or the logical product |
|
The
"or", the disjunction or the logical sum |
|
Logical
negation |
|
|
|
|
|
|
|
The
Fundamental Laws of the Algebra of Sets |
| associative
law:
(A
U B)
U C
= A
U (B
U C)
and
(A ∩ B) ∩ C
= A ∩ (B ∩ C
) |
| commutative
law: A
U B
= B U A
and
A ∩ B
= B
∩ A |
| distributive
law:
A
U (B ∩ C) = (A U B) ∩ (A U C)
and
A ∩ (B U C) = (A ∩ B) U (A ∩ C) |
| De
Morgan's laws: (A
U B)'
= A' ∩ B'
and
(A ∩ B)'
= A' U B' |
|
|
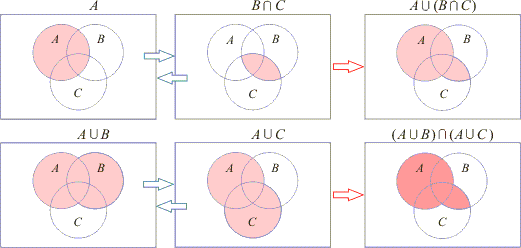
| The
distributive law A
U (
B ∩ C
) = ( A U B
) ∩ (
A U C
) shown
by Venn Diagrams: |
 |
|
| Sets
and Logic |
| In logic a statement
is a sentence that is either true or false, but not both. The
truth or falsity of a statement is called its truth value. Truth
values can be represented as binary numbers, where 0 denotes
false and 1 denotes true. |
| Compound
statements or proposition are two or more simple statements
joined by connectives. Two
connectives used to make compound statements are the words
and and or. |
| The compound statement formed by the
word and is called the conjunction or the logical
product, and denoted as p
Λ
q.
A conjunctive statement is true only if its statements
(components) are both true. |
| The
compound statement formed by the word or is called
the disjunction
or the logical sum, and denoted as
p
V
q.
A disjunctive statement is true if
either or both of its statements is true, and false only when
both are false. |
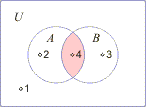
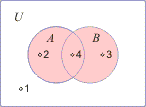
| The
truth tables for the compound statements, p
Λ
q and p
V
q,
and corresponding Venn
Diagrams for the intersection and the union are shown
below. |
| |
p |
q |
p
Λ
q |
| 1 |
0 |
0 |
0 |
| 2 |
1 |
0 |
0 |
| 3 |
0 |
1 |
0 |
| 4 |
1 |
1 |
1 |
|
|
|
| |
p |
q |
p
V
q |
| 1 |
0 |
0 |
0 |
| 2 |
1 |
0 |
1 |
| 3 |
0 |
1 |
1 |
| 4 |
1 |
1 |
1 |
|
|
|
| Observe
coincidence between the four combinations
in the truth tables and the corresponding four
numbered areas in the Venn
Diagrams, so |
| -
first combination, that describe the case when an element
doesn't belong to the set A
nor B,
correspond to the part of the
universal
set excluding areas of A
and B,
numbered 1. |
| -
second combination, that describe the case when an element
belong to the set A
but not to B,
correspond to the part of the set A
which is not in B,
numbered 2.
|
| -
third combination, when an element
belong to B
but not to A,
correspond to the area that is numbered 3. |
| -
forth combination, when an element
belong to A
and B,
correspond to the area that is numbered 4 and which is
shared region between the sets A
and B. |
| Logical negation "not
p"
or ~p
denotes negation
of an statement p.
Thus the truth value of the negation of any statement is
always opposite of the truth value of the given
statement, as is shown in the truth table. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Beginning
Algebra Contents |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
