|
| Boolean
Algebra |
|
|
|
|
|
Boolean algebra |
Definition |
|
Basic
theorems |
|
Boolean
operations on sets |
|
|
|
|
|
|
| Definition |
| Properties
of both set operations and logic operations are used in an
algebraic structure called a Boolean algebra. |
| A
Boolean algebra is a set A
on which are defined; two binary operations, + (called OR),
·
(called AND), a unary operation, denoted '
(called NOT) and two distinct
elements 0 and 1, such that, for all elements a,
b
and c
of the set A,
the following axioms hold: |
|
| associative
law:
a + (b + c)
=
(a + b) + c
a ·
(b ·
c) = (a ·
b) ·
c |
| commutative
law:
a + b
= b + a
a ·
b = b
·
a |
| distributive
law:
a + (b ·
c) = (a + b) ·
(a + c)
a ·
(b + c) = (a ·
b) +
(a ·
c) |
| identity
law:
a + 0 = a
a ·
1
=
a |
| complement
law:
a + a' = 1
a ·
a' = 0 |
|
| From
these axioms derived are following identities: |
| idempotent
law:
a + a
=
a
a ·
a = a |
| boundedness
law:
a + 1
=
1
a ·
0 = 0 |
| absorption
law:
a + (a ·
b) = a
a ·
(a + b)
=
a |
| involution
law:
( a' )' = a |
| De
Morgan's
laws:
(a + b)'
= a' ·
b'
(a ·
b)' = a' + b' |
| 0
and 1 complements: 0'
=
1
1' = 0 |
|
| Boolean
Operations on Sets |
| Using
noticed coincidence between truth tables and Venn's diagrams we
can prove any of the axioms or theorems of Boolean algebra.
Thus, below is shown the proof of the distributive law: |
|
A
· ( B
+ C
) =
A
· B
+ A
· C
|
| |
A |
B |
C |
B
+ C |
A
·
( B
+ C ) |
| 1 |
0 |
0 |
0 |
0 |
0 |
| 2 |
1 |
0 |
0 |
0 |
0 |
| 3 |
0 |
1 |
0 |
1 |
0 |
| 4 |
0 |
0 |
1 |
1 |
0 |
| 5 |
1 |
1 |
0 |
1 |
1 |
| 6 |
1 |
0 |
1 |
1 |
1 |
| 7 |
0 |
1 |
1 |
1 |
0 |
| 8 |
1 |
1 |
1 |
1 |
1 |
|
| A |
B |
C |
A
·
B |
A
·
C |
A
·
B
+ A
·
C |
| 0 |
0 |
0 |
0 |
0 |
0 |
| 1 |
0 |
0 |
0 |
0 |
0 |
| 0 |
1 |
0 |
0 |
0 |
0 |
| 0 |
0 |
1 |
0 |
0 |
0 |
| 1 |
1 |
0 |
1 |
0 |
1 |
| 1 |
0 |
1 |
0 |
1 |
1 |
| 0 |
1 |
1 |
0 |
0 |
0 |
| 1 |
1 |
1 |
1 |
1 |
1 |
|
|
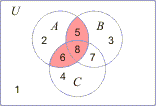
| Notice
that required Boolean (binary) operations are performed
on the three sets so, in the above tables there are 23 =
8 combinations. In both tables, at the resultant
columns, obtained are ones (1) for the same combinations
of input values of the sets, A,
B
and C,
which correspond with the
three colored areas in the Venn's diagram. |
 |
|
| Using
rules of Boolean algebra each of the eight areas of the
Venn's diagram can be represented as a product involving given
sets, A,
B
and C: |
|
| 1 |
A'
·
B'
·
C' |
3 |
A'
·
B
·
C' |
5 |
A ·
B
·
C' |
7 |
A'
·
B
·
C |
| 2 |
A
·
B'
·
C' |
4 |
A'
·
B'
·
C |
6 |
A ·
B'
·
C |
8 |
A ·
B
·
C |
|
| In
general, the following rules must always be followed when
evaluating a Boolean expression:
|
| 1.
First, perform all complementations of single terms.
|
|
2. Then perform all operations within parentheses.
|
|
3. Perform an AND operation before an OR operation unless
parentheses indicate otherwise.
|
|
|
|
|
|
|
|
|
|
|
|
|
| Beginning
Algebra Contents |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
