|
| Graphing
Linear Equation, Linear Function (First Degree Polynomial)
|
|
|
|
 Linear
function f (x) = mx + c
Linear
function f (x) = mx + c |
| The
graph of the linear function |
| Slope
or gradient, y-intercept and x-intercept |
|
|
|
|
|
|
| Linear function f
(x)
= mx
+ c |
| The expression |
| y =
mx
+ c
or f
(x)
= ax + b
|
| we call linear function,
where x
is the argument or the independent variable, f
(x) or
y
is the dependent variable or the function, numbers, a and
b
or m and
c are
constants. |
| If the coefficient
m =
0, then y does not depend of
x. |
| Linear
function f
(x)
= mx
+ c,
m is
not 0, to
each value of the argument
x associates a unique value
of y. |
|
| The graph of the linear function |
| A function
y =
f
(x)
can be considered as the set of ordered pairs (x,
y) where each pair
represents a point in a Cartesian coordinate system xOy. |
| When plotted on an
x,
y graph linear function forms a
straight line. |
| The constant
m is called the
slope or gradient
and the constant c is the
y-intercept.
This is the point of intersection between the graph of the
function and the y-axis. |
| If the coefficient
m is
not 0 and c =
0
then, the linear function has the form y
=
f
(x) =
mx. |
|
To the graph of the
function f (x) =
mx belong the points
P (x,
mx
) of a coordinate plane of which the abscissas are values of
argument x
taken arbitrarily, and the ordinates are the calculated values
of the function.
|
| Thus, for
x =
0 =>
f (x) =
f
(0)
=
m
· 0
=
0,
this means that the graph of the function f
(x) =
mx
is running through the origin
O(0,
0) or
the x-intercept
is at the origin. |
|
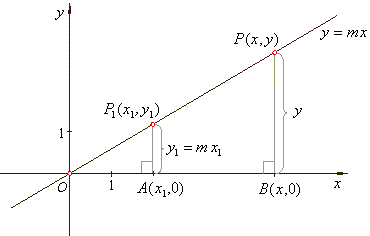 |
|
| As the above
right triangles OAP1
and OBP
are similar the ratios of the ordinates and the abscissas of the
points
P and
P1
are equal: |
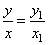 |
or |
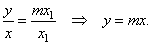 |
|
| The
value of the ratio |
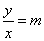 |
|
|
|
determines the rate at which the y-coordinate of a straight line
changes with respect to the x-coordinate. |
| On a line graph, changing
m
makes the line steeper or more gentle (shallower). |
| If m
is negative, y
decreases
as x
increases. |
|
| Example:
Find the equation of the line that passes through the
origin and the point A(-3,
2). |
| By
plugging the coordinates of the point A
into the equation y =
mx we
determine the slope m. |
|
|
|
|
|
|
|
|
|
|
|
|
|
| Beginning
Algebra Contents C |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |