|
| Graphing
Linear Equation, Linear Function (First Degree Polynomial)
|
|
|
|
Slope-intercept form of a line
|
|
Properties
of the linear function
|
|
|
|
|
|
|
| Slope-intercept form of a line
|
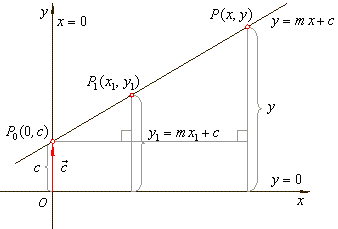
| By moving the graph of the linear function
f (x)
= mx
vertically by
the vector c, |
| obtained is the linear function |
f
(x)
= mx
+ c, |
|
|
| every
point of which has the y value that differs from the source graph
f (x)
= mx by
the same constant c. |
| This form of the linear function is called the
slope-intercept form. |
|
 |
|
| The graph of the function
f (x)
= mx
+ c
intersects the y-axis at the
point P0(0,
c). |
| Every point on the
y-axis has abscissa
0 that is, |
x
= 0 |
denotes the
y-axis. |
|
|
| Thus, we find the
y-intercept by calculating
f
(0)
= m
· 0
+ c,
f
(0)
= c. |
| Every point on the
x-axis has ordinate
0 that is, |
y
= 0 |
denotes
the
x-axis. |
|
|
| Therefore, the intersection point of the
graph and the x-axis we calculate from the equation
f (x)
= 0. |
| Thus
solving for x, |
0
= mx
+ c, |
we get |
 |
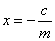the root or
the zero point or the x-intercept |
|
| of the
linear function f
(x)
= mx
+ c. |
|
| Example:
Find the equation of the line that passes through the points A
(-4,
-1)
and B (6,
4). |
|
|
|
|
| Properties
of the linear function
|
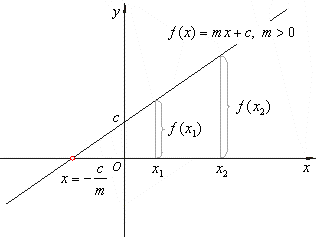
| We examine the behavior of a function
y =
f
(x)
by moving from left to right in the direction of x-axis by inspecting its graph. |
| The linear
function f (x)
= mx
+ c,
m
> 0 is increasing, the graph rises from left to right, that is, |
| f
(x1)
< f
(x2)
for all
x1
< x2 |
 |
|
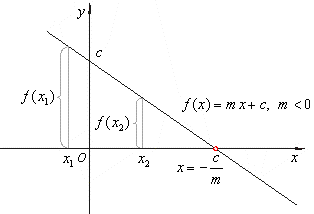
| If
m
< 0 linear function decreasing,
f
(x1)
> f (x2) for all
x1
< x2 i.e., the graph falls from left to right. |
|
 |
|
|
|
|
|
|
|
|
|
|
|
| Beginning
Algebra Contents C |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
