| |
| The Rectangular (Two-dimensional,
Cartesian) Coordinate System |
|
|
|
| |
Rectangular coordinate axes, x-axis
and y-axis,
origin, quadrants
|
|
Ordered
pair (x, y), coordinates of a point (abscissa x, ordinate y) |
|
Midpoint of a line segment
|
|
|
|
|
|
|
| Rectangular coordinate axes, x-axis
and y-axis,
origin, quadrants
|
| The Cartesian coordinate system is defined by two
axes at right angles to each other, forming a plane. |
| The horizontal axis is
labeled x, and the vertical axis is labeled
y. |
| The point of intersection,
where the axes meet, is called the origin labeled O. |
| Given each axis,
choose a unit length, and mark off each unit along the axis, forming
a grid. |
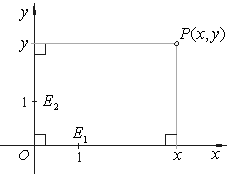
| The position of each point in a plane is identified with an
ordered pair of real numbers, in the form (x,
y),
called the
coordinates of the point. |
|
| The
x-coordinate, called the
abscissa, equal to the distance of the point from the y-axis measured parallel
to the x-axis, and the
y-coordinate, called the
ordinate, the distance of the point from the x-axis measured parallel to the
y-axis.
The
origin O
has coordinates (0, 0). |
|
 |
|
|
|
| The intersection of the two axes creates four quadrants
indicated by numerals I, II, III, and IV. The quadrants are labeled
counterclockwise starting from that in which both coordinates are
positive. |
 |
|
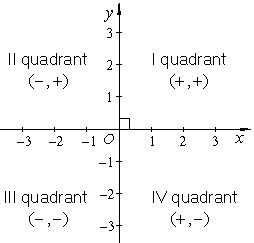| Ordered pair (
x,
y
),
coordinates of a point (abscissa x, ordinate y)
|
| On the Cartesian plane the points are placed as shown: |
|
A( 3, 0 ), B( 2, 3 ), C( -
5/2, 4 ), D( 0, 2
), E( - 4,
0 ), F( -2,
-11/3
), G( 0, -1
), and H( 4, -2
). |
 |
|
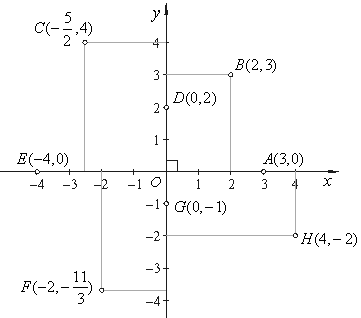| Midpoint of a line segment
|
| The coordinates of the midpoint
M(xM,
yM)
of the line segment AB
where, A(x1,
y1)
and B(x2,
y2)
are endpoints: |
|
|
|
|
| Example:
Find the midpoint of the
line segment AB
where the endpoints, A(-5,
3)
and B(-1,
-1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
|
|
