|
| Linear
Inequalities |
|
|
|
| Linear
inequalities |
Inequality signs
|
|
Properties
of inequalities
|
|
Solving
linear inequalities |
|
|
|
|
|
|
| Inequality signs
|
| Inequality
is a statement about the relationship between two numbers or
quantities that holds when they are comparable and related by
ordering but are not equal. |
| These
relationships are written as: |
|
a
< b
meaning
a
is
less than b, |
|
a ≤
b meaning
a
is
less than or equal to b, |
|
a
> b
meaning
a
is
greater than b, |
|
a ≥
b meaning
a
is
greater than or equal to b. |
|
| Properties
of inequalities
|
| The
trichotomy property of the real
line states that for any real numbers, a
and
b,
exactly one of |
|
a
< b,
a = b,
a
> b,
is true. |
|
| The
transitive property of inequalities
states that for any real numbers, a,
b and
c, |
|
if a
< b
and b
< c,
then
a
< c, |
|
if a
> b and
b
> c,
then
a
> c. |
|
| The
addition and subtraction property
of inequalities states that for any real numbers, a,
b and
c, |
|
if a
< b,
then
a
+ c
< b
+ c,
and a
-
c
< b
-
c, |
|
if a
> b,
then
a
+ c
> b
+ c, and
a
-
c
> b
-
c. |
|
| The
multiplication and division
property of inequalities states that for any real numbers, a,
b and
c, |
|
if c
is
positive and
a
< b,
then
a
· c
< b
· c,
and a/c
< b/c, |
|
if c
is
negative and
a
< b,
then
a
· c
> b
· c,
and a/c
> b/c. |
|
| The
sense of an inequality is not changed if both sides are
increased or decreased by the same number, or if both sides are
multiplied or divided by a positive number. |
| The sense of an
inequality is reversed if both sides are multiplied or divided
by a negative number. |
|
| The
additive inverse property of inequalities states that for any real
numbers a
and
b, |
|
if
a
< b
then
-a
>
-b, |
|
if
a > b
then
-a
< -b. |
|
| The
multiplicative inverse
property of inequalities states that for any real numbers a
and
b
that are both positive or both negative, |
|
|
if
a
< b
then
1/a
>
1/b, |
|
if
a > b
then
1/a
<
1/b. |
|
| Note that, the above properties also hold if strict inequality signs, < and >, are replaced with their corresponding non strict
inequality signs, ≤
and ≥. |
|
| Solving
linear inequalities
|
| A linear inequality has the standard form
ax +
b
> 0, where a,
b
Î
R |
| and where other inequality
signs like <, > and < can appear. |
| As with equations, the inequality is solved when positive x is isolated on the left. |
| The solutions to an inequality are all values of
x
that make the inequality true. |
| We may add the same number to both sides of an inequality. |
| By multiplying both sides of an inequality
by the same negative number, the sense of the inequality changes, |
|
i.e., it reverses the direction of the inequality sign. |
|
| Example: |
 |
|
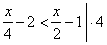x -
8
< 2x
-
4 |
|
- x
<
4
|
·
(-1) |
|
x
>
-4 |
|
 |
| The
solution of the inequality is every real number greater
than -4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Beginning
Algebra Contents C |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
