|
| Polynomial |
|
|
|
 Terms
and the degree of a polynomial
Terms
and the degree of a polynomial |
 Addition and subtraction of
polynomials
Addition and subtraction of
polynomials
|
 Multiplication of polynomials
Multiplication of polynomials
|
 Division of polynomials
Division of polynomials
|
|
|
|
|
|
|
| Polynomial |
| Terms
and the degree of a polynomial |
| The
polynomial is mathematical expression consisting of a sum of
terms each of which is a product of a constant and one or more
variables raised to a non-negative integral power. If there is
only a single variable x, the general
form is given by |
|
anxn + an-1xn-1 + an-2xn-2
+ . . . + a2x2
+ a1x + a0, |
| where
the ai
are real
numbers called coefficients and a0
is the constant term. |
| The
degree of a polynomial is the highest power or the sum of powers
in any term of a given polynomial or algebraic expression. |
|
| Addition and subtraction of
polynomials
|
| We
add or subtract polynomials by combining their like
terms. The like terms are terms that have the same
variables raised to the same exponents. |
|
| Example:
a)
( -
5x3 +
2x2
- x +
4) + ( -
4x2 +
3x - 7)
= - 5x3 +
(
2 -
4) · x2 +
(
-1
+
3) · x +
4 - 7
= |
|
= - 5x3 - 2x2 +
2x - 3 |
|
|
b) (
x4 -
3x3
+
5x - 1)
-
( - 2x4 +
x3
- 3x2 +
4)
= x4 -
3x3
+
5x - 1
+ 2x4 -
x3
+
3x2 -
4
= |
|
= (
1 +
2) · x4
+ (
-3
- 1)
· x3
+
3x2
+
5x - 5
= 3x4 -
4x3
+
3x2
+
5x - 5 |
|
| Multiplication of polynomials
|
| When
multiplying two polynomials together, multiply every term of one
polynomial by every term of the other polynomial using
distributive property. |
|
| Example:
( -
2x3 +
5x2
- x +
1) ·
(
3x - 2)
= |
|
= 3x · (
- 2x3)
+ 3x · 5x2
+ 3x ·
(-x) + 3x · 1
+ (- 2) · ( -
2x3)
+ (- 2) · 5x2
+ (- 2) · ( -x)
+ (-
2) · 1
= |
|
= - 6x4
+ 15x3
- 3x2
+ 3x +
4x3 -
10x2
+ 2x -
2 = -
6x4
+ 19x3
-
13x2
+ 5x -
2 |
|
| Division of polynomials
|
| Divide
the highest degree term of dividend by the highest degree term
of the divisor to get the first term of the quotient. |
| Take the first term of the quotient and multiply it by every term of divisor.
Write this result below the dividend, making sure you line up all the terms with the terms of the dividend that has the same degree. |
| Subtract the result from the dividend, i.e., reverse all the signs of the terms of the result and add like terms. |
| Repeat the process of long division until the degree of the new obtained dividend is less than the degree of the divisor. |
|
|
| Note,
since each second line should be subtracted, the sign of each term is reversed. |
|
|
b)
(
3x4 +
x2 +
5) ¸
( x2 -
x -
1) = 3x2 + 3
x +
7 |
|
|
|
|
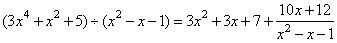 |
|
| |
|
| like |
17 ¸
5 = 3 +
2/5 |
| |
-15 |
| |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
| Beginning
Algebra Contents C |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |