|
|
|
|
Linear
equations |
 Linear
equation
Linear
equation |
 Solving linear equations
Solving linear equations |
 Applications
of linear equations, word problems
Applications
of linear equations, word problems |
|
Numbers word problem |
|
Geometry and physics word problems
|
|
|
|
|
|
|
| Linear
equation |
| An equation is linear if it can be written in the form |
| ax =
b,
where
x
is the variable and a and
b are constants. |
| A linear, means the
variable x appears only to the first power. |
| The solution of an
equation is the value of the variable x that makes the equation a
true statement. |
|
| Solving linear equations |
| We solve an equation by transforming it through a
sequence of equivalent equations, statement by statement, until x
finally is isolated on the left. |
| Two equations that have the same
solutions are called equivalent. |
| Shift a number from one side of an
equation to the other, by writing it on the other side with the inverse
operation. |
| When the operations are addition or subtraction a term
may be shifted to the other side of an equation by changing its sign. |
| After solving an equation check the solution by substituting them in
the original equation. |
|
| Examples:
a)
-1
-
(2
-
x)
= 2
-
(3x
+
1) |
|
-1
-
2
+
x
= 2
-
3x
-
1 |
|
x
+
3x
= 2 +
2 |
|
4x
= 4
|
¸
4 |
|
x
= 1 |
|
|
|
|
| Applications of the linear
equations,
word
problems
|
| Word problems - translate the words into mathematics |
| Numbers word
problem |
| Example:
The sum of two digits of a two-digit number is 10. If the digits are
reversed, the new number is |
|
four less then five times the original number. Find two-digit number. |
| Solution:
Let
x be
tens place value digit then,
10
-
x is units digit, thus given number is
10x
+ (10
-
x). |
| By reversing digits we get
10
· (10
-
x)
+ x. |
| Hence
given problem yields: 10
· (10
-
x)
+ x
= 5
· [10x
+ (10
-
x)]
-
4 |
|
100
-
10x
+ x
= 5
· [9x
+ 10]
-
4 |
|
100
-
9x
= 45x
+ 50
-
4 |
|
54x
= 54
| ¸
54 |
|
x
= 1
thus,
the two-digit number is:
10x
+ (10
-
x)
=19. |
|
| Geometry and physics word problems
|
| Example:
A rectangle has the perimeter
90 cm and the width 13 cm less then the length. |
|
What is the area of the rectangle? |
|
|
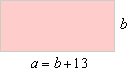 |
|
a
= b
+ 13
= 16
+
13
= 29
cm |
| A
= a
· b
= 29
·
16
= 464
cm2 |
|
| the perimeter
P
of a rectangle: |
| P
= 2
·
(a
+ b)
= 90 |
|
2
·
(b + 13
+ b)
= 90
| ¸
2 |
|
2b
+ 13
= 45 |
|
2b
= 32 |
|
b
= 16
cm |
|
|
|
| Example:
After a car A started traveling at a speed of 90 km/h, half-hour later
from the same place in the |
|
same direction starts car B traveling at 120 km/h. When will car B reach the car A? |
|
|
Solution:
The cars are traveling the same distance
d
= r
· t .
distance = rate x time |
|
The car A takes x hours, and the car B,
x
- 1/2
hours. |
|
Thus, 90
· x =
120
· (x
- 1/2)
| ¸
30 |
|
3x
=
4x
- 2 |
|
x
=
2
hours, the car B will reach the car A after
x
- 1/2 =
2
- 1/2 =
3/2 hours. |
|
|
|
|
|
|
|
|
|
|
|
|
| Beginning
Algebra Contents C |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |