|
| Percentage,
percent
|
|
|
|
|
Percent, decimal number and
fraction conversions |
|
Percent - base, rate and portion (part or
amount)
|
|
Basic percent formulas |
|
Percent problems
|
|
Percent
increase or decrease
|
|
|
|
|
|
|
| Percent, decimal number and
fraction conversions |
| A percent (per cent) is a ratio or a fraction with 100 as the
denominator, represented by the symbol %, |
| |
written |
 |
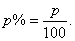Realize
that |
 |
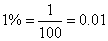for
example, |
 |
|
|
|
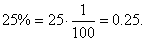| Conversions between a percent, a decimal number and a fraction
are shown below. |
|
|
|
| Percent - base, rate and portion (part
of
amount)
|
| We use percentage to express relationship between two quantities
or their parts taking 100 as the base of a comparison. |
| While
comparing, the quantity (or the number) of which we compute the percent we consider as a whole or
100% of an amount, and call it
the base or initial value (x). |
| The number of percent is the
rate (p).
The portion of the base value expressed as the percent of it is the
part (y)
of
amount. |
| The formal way to solve a percentage problems is
by using proportion, |
| |
part
: base (whole) = rate : 100 |
or |
y
: x =
p
: 100. |
|
|
|
| Percentage formulas |
| Thus, from the proportion we calculate,
the part of whole (or amount) y,
the rate p
and the base value x: |
|
the part or amount |
 |
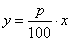the rate |
 |
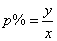the base
(initial) value |
 |
|
|
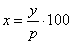| Example: |
What is 25% of 80? |
| x =
80,
p%
= 25%,
y =
? |
|
 |
|
|
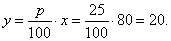| The percent represents relationship between a part and the whole. |
| Example: |
What percent of 80 is 20? |
|
y =
20,
x =
80,
p%
=
? |
|
 |
|
|
| |
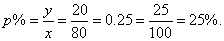The base value |
|
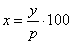therefore |
 |
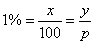represents
1% of the base value. |
|
|
|
| Example: |
What is the base value if 25% of it is 20? |
|
p%
= p/100 = 25%,
y =
20,
x =
? |
|
 |
|
|
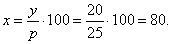| Percent
increase or decrease
- base (x),
amount (y),
percent (p) |
| |
from |
x
: 100
=
( x
±
y )
: ( 100
±
p) |
and |
y
: p
=
( x
±
y )
: ( 100
±
p) |
|
|
| where
x
±
y denotes
original or base value x increased or decreased by amount
y |
|
|
|
| Example: |
In the price of $33 included is tax of 10%. |
| What is net price? |
|
 |
|
|
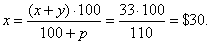| Example: |
Price reduced by 20% amounts
to $320. |
| How much is reduced? |
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
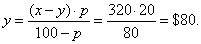| Beginning
Algebra Contents B |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
