135
 
Integral calculus
  Differentiation and integration of infinite series
If  f (x) is represented by the sum of a power series
with radius of convergence r > 0 and  - r < x < r, then the function has the derivative
and the function has the integral

Thus, a power series can be differentiated and integrated term by term while the radius of convergence remains the same, with only (possible) exception at the endpoints of the interval of convergence.

  Differentiation and integration of infinite series examples
 Example:  Represent the  f (x) = arctan x  or   f (x) = tan -1 x,  by a power series.
 Solution:  Since
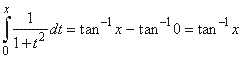thus, we should integrate the series
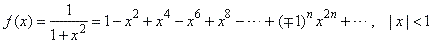Let write down the initial sequence of nth order polynomials that describe the function inside the interval of convergence  -1 < x < 1,
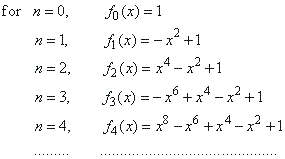Since every polynomial above is missing the preceding odd degree term, their coefficient  an-1 = 0
thus, the coordinates of translations

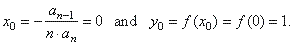Therefore, the polynomials that describe the function all are source polynomials of even degree translated in the direction of the y axis by  y0 = 1, as is shown in the picture below.

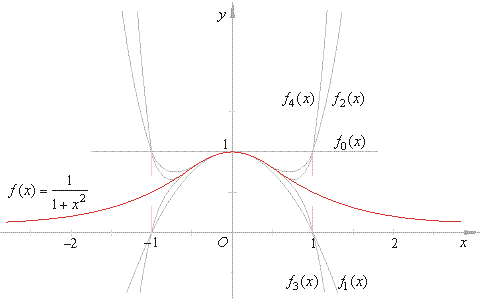The above graph shows that all evenly indexed polynomials (with the positive leading coefficient) intersect at (-1, 1) and (1, 1) while all polynomials with odd indexes, with the negative leading coefficient, intersect at (-1, 0) and (1, 0).

Thus, they will never reach the functions values  f (-1) = 1/2 and  f (1) = 1/2, though their graphs come closer and closer to the points (-1, 1/2) and (1, 1/2) as n increases.
Then by integrating the series
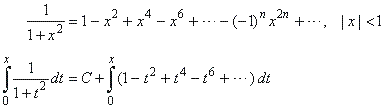and since for x = 0 the integral is zero then, C = 0 therefore
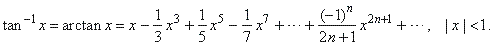From where, for x = 1 

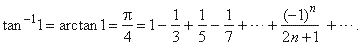Let write down the initial sequence of nth order polynomials, which describe the  f (x) = arctan x by the above power series inside the interval of convergence  -1 < x < 1,

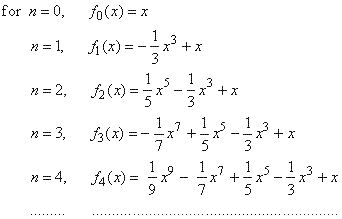Since every polynomial above is missing the preceding even degree term, their coefficient  an -1 = 0
thus, the coordinates of translations
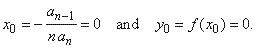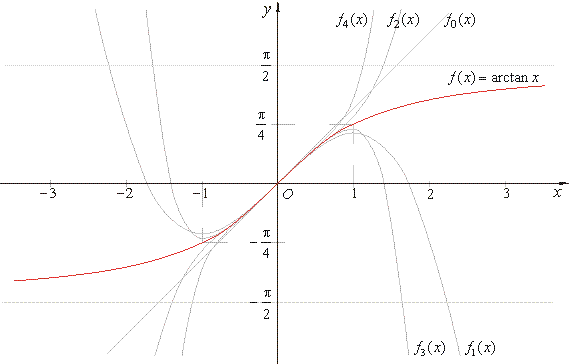
Therefore, the polynomials that describe the function all are source polynomials of odd degree, as shows the picture below.
Note that all polynomials in the series with odd indexes have extreme points at  x = -1 and  x = 1.
 Differentiation and integration of power series
Recall that the exponential function  f (x) = ex represented by the power series
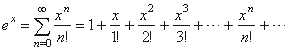is absolutely convergent for all real x since
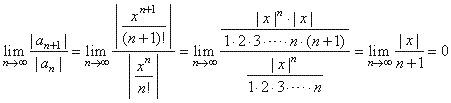the limit L < 1 for any value of x.
  Applying the power rule
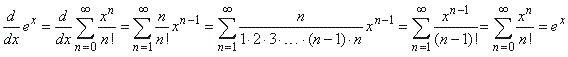thus, for all real x the function f (x) = ex is equal to its own derivative  f ' (x).
 Example:  Find 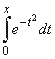by representing the integrand function as the power series.
 Solution:  By substituting  - x2  for x in the above power series expansion of  ex we get
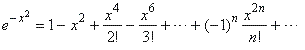Let write down the initial sequence of nth order polynomials that describe the function for all real x,
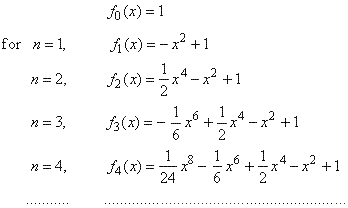Since every polynomial above is missing the preceding odd degree term, their coefficient  an-1 = 0
thus, the coordinates of translations
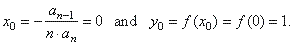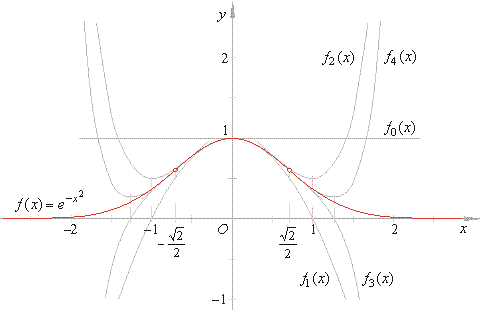
Therefore, the polynomials that describe the function all are source polynomials of even degree translated in the direction of the y axis by  y0 = 1, as is shown in the picture below.
Note that the roots of odd indexed polynomials in the series correspond to the abscissas of successive even indexed polynomials, as shows the above graph.
On the graph of the bell-shaped curve, representing the probability density function of a normal distribution, at x = ± Ö2/2 denoted are the points of inflections.
  Therefore, the power series representing the normal curve converges for all real x.
Hence, by integrating the series term by term obtained is
 
 
 
 
 
 
 
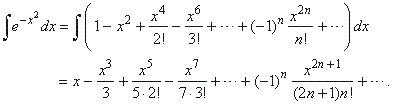Contents N
 
 
 
 
Copyright © 2004 - 2020, Nabla Ltd.  All rights reserved.