|
|
|
|
Integral
calculus
|
|
|
|
Definite
integrals
|
|
Substitution
and definite integration
|
|
When
we evaluate an indefinite integral of the form
|
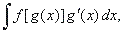 |
|
| we
use the substitutions g
(x)
= u and g'
(x) dx = du
to obtain |
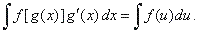 |
|
| Therefore,
to evaluate the definite integral using substitution
|
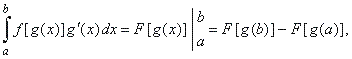 |
|
or
|
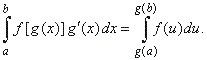 |
|
|
| Note,
by making substitution the definite integral changes the limits of
integration. |
| That is, the new limits of
integrations
must correspond to the range of values for u
as we now integrate the simpler integrand f
(u)
from ua
= g (a)
to ub = g
(b).
|
|
|
Substitution
and definite integration examples
|
| Example:
Evaluate |
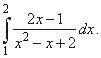 |
|
|
|
|
| Example:
Evaluate |
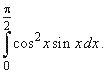 |
|
|
|
|
|
Integrations
by parts and the definite integral
|
| If
u
(x)
and v
(x)
are continuous functions with continuous derivatives on [a,
b], then |
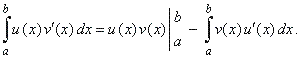 |
|
| Example:
Evaluate |
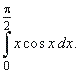 |
|
|
|
|
|
The
improper integrals
|
|
A
definite integral with one or both limits of integration infinite,
or having an integrand that becomes infinite between
the limits of integration is called the improper
integral.
|
| Let
f (x)
be defined on [a,
oo
)
and integrable on [a,
b] for all a
< b <
oo,
then
|
|
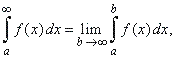 |
provided
the limit exists.
|
|
| If
f (x)
is defined on ( -
oo,
b] and integrable on [a,
b] for all -
oo
< a < b,
then
|
|
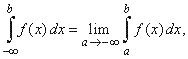 |
provided
the limit exists.
|
|
|
If
f (x)
is defined on ( -
oo,
oo
)
and integrable on any closed interval [a,
b], then
|
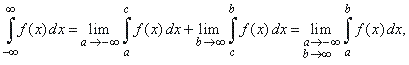 |
| provided
the limits on the right exist.
|
| In
each case where the appropriate limit exists we say the integral
converges, otherwise the integral is said to diverge. |
|
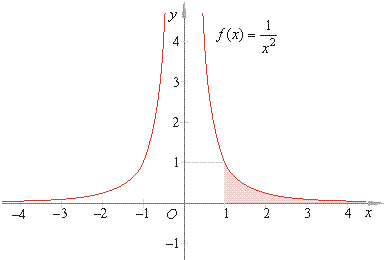
| Example:
Evaluate |
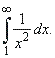 |
|
|
|
|
|
As
the area of the region beneath the graph of f
over the interval [1,
b] as b
goes to infinity A
= 1, thus the integral
converges.
|
|
| Example:
Evaluate |
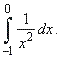 |
|
|
|
|
|
Therefore,
the integral diverges.
|
|
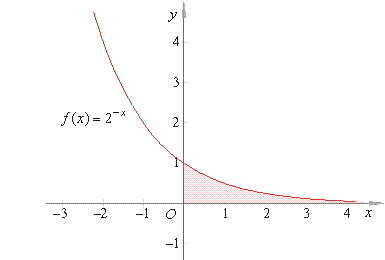
| Example:
Evaluate |
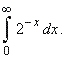 |
|
|
|
|
|
Therefore,
the integral converges.
|
|
| Example:
Evaluate |
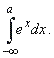 |
|
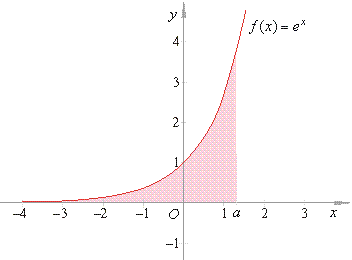
|
|
|
|
Therefore,
the integral converges.
|
|
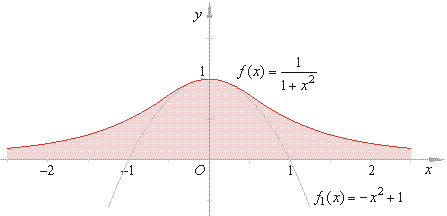
| Example:
Evaluate |
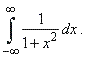 |
|
|
|
|
|
Therefore,
the integral converges.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Contents
N
|
|
|
|
|

|
|
|
|
|
|
Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved.
|
|
|