|
|
|
|
Integral
calculus
|
|
|
|
Applications
of the definite integral
|
|
The
area of a region in the plane - The
area between the graph of f(x) and the x-axis
|
|
If
given a continuous nonnegative function f
defined over an interval [a,
b] then, the area A
enclosed by the curve y
= f (x),
the vertical lines,
x
= a and
x
= b and the x-axis,
is defined as
|
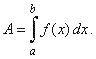 |
|
|
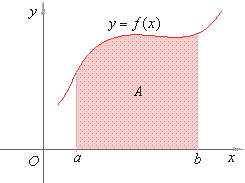 |
|
|
The
area between the graph of a curve and the coordinate axis examples
|
| Example:
Find the area between
the graph of f
(x) = -
(1/3)x3 + 3x
and the x-axis
over the interval defined by two nonnegative successive
roots of the given cubic function.
|
| Solution:
To
find roots we should solve f
(x) = 0,
|
|
|
|
| Example:
Find the area between
the curve x = -
y2 + y
+ 2 and the y-axis.
|
| Solution:
Since
given curve is the parabola whose axis of symmetry is
parallel to the x-axis
we first calculate its
y-intercepts
by setting x =
0 to determine the limits of
integration,
|
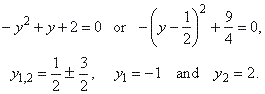 |
| Thus,
the area |
|
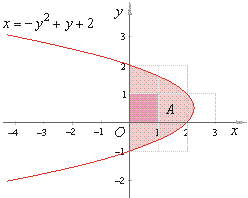 |
|
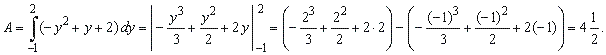 |
|
| Example:
Find the area of the
ellipse b2x2 +
a2y2 = a2b2
that is symmetrical about
the coordinate axes and that intersects the coordinate axes at the
points (+ a,
0) and (0,
+
b).
|
| Solution:
Let
write the ellipse in the explicit form y
= f (x)
|
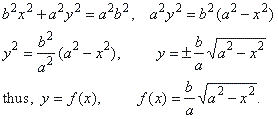 |
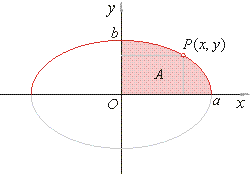
| Thus,
we calculate the area A
using the solution of the
indefinite integral, that is |
|
 |
|
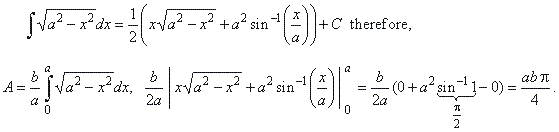 |
| Hence, the area of the ellipse is abp,
and by setting b
= a we get the area of
the circle
a2p.
|
|
| Example:
Find the area A
enclosed
by the parabola, the line and the x-axis
shown in the below figure.
|
| Solution:
First we should find
the equation of the parabola and the line using given points.
|
| The parabola is translated in the
direction of the x-axis
by x0
= 1, so
that
|
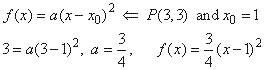 |
| and the line |
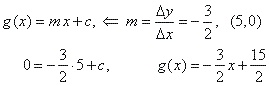 |
| Thus,
the area |
|
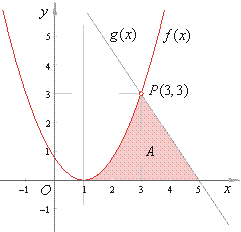 |
|
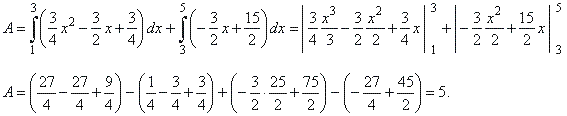 |
|
|
The
area bounded by a parametric curve
|
|
If
a curve is given by the parametric equations x
= f (t) and
y = g (t), then
the area enclosed by the curve,
the vertical lines, x
= a and x
= b and the x-axis,
we
obtain from
|
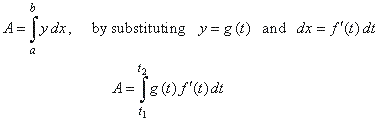 |
| where,
f (t1) = a
and f (t2)
=
b,
g (t)
>
0
inside
[t1,
t2].
|
|
| Example:
Find the area bounded
by the
ellipse x = a
cos t,
y = b
sin t,
( 0 <
t <
2p
).
|
| Solution:
As the ellipse is symmetrical about
the coordinate axes we will calculate quarter of the area.
|
| By substituting
x
= 0 and x
= a into the
equation x = a
cos t and
solving for
t,
we get the limits of integration
t1 =
p/2
and t2 =
0
respectively. Therefore,
|
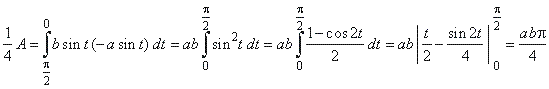
|
| so that, the area of the ellipse
A = abp.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Contents
N
|
|
|
|
|

|
|
|
|
|
|
Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved.
|
|
|