|
|
|
|
ALGEBRA
|
|
|
|
Graphs of polynomial functions
|
|
::
Quadratic
function, the second degree polynomial f
(x)
= a2x2
+
a1x + a0
|
|
By plugging the coordinates of translations into the
source quadratic function f
(x)
= a2x2
we get
|
|
f (x)
=
y
=
a2x2
+
a1x + a0
or y
-
y0
= a2(x
-
x0)2
|
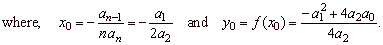
|
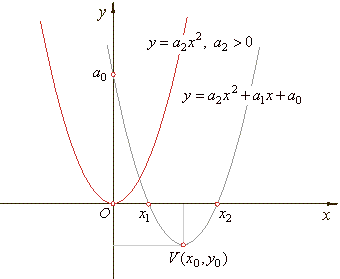
|
|
By
setting x0
= 0 and y0
= 0
obtained is the
source quadratic
y
= a2x2
.
|
| If
a2
·
y0
<
0
then
the roots are |
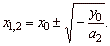 |
The turning point
V (x0
, y0
).
|
|
|
|
::
Quadratic
equation, quadratic formula |
| The
zeros of a polynomial function are the values of x
for which the function equals zero. |
| Therefore, the solutions of the equation
f (x)
= 0,
that are called roots of the polynomial, are the zeros of the
polynomial function or the x-intercepts of its
graph in a coordinate plane. Let solve the equation, |
| a2x2
+
a1x + a0
= 0
or ax2
+ bx + c
= 0 |
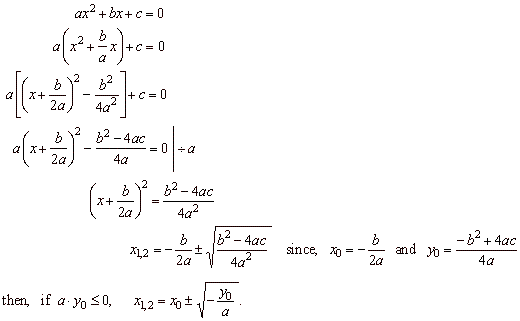 |
|
|
:: Cubic
function, the third degree polynomial f
(x)
= a3x3
+ a2x2
+
a1x + a0
|
|
By plugging the coordinates of translations into the
source cubic function f
(x)
= a3x3
+
a1x
we get
|
|
f
(x) =
a3x3
+
a2x2
+
a1x + a0
or y
-
y0
= a3(x
-
x0)3
+
a1(x
-
x0)
where,
|
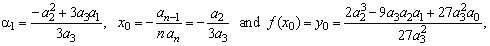
|
|
by
setting x0
=
0 and y0
= 0 we get
the source cubic function
y
= a3x3
+
a1x
where a1=
tan at
.
|
|
Coordinates
of the point of inflection coincide with the coordinates of
translations, i.e., I
(x0,
y0).
|
|
The source cubic functions are
odd functions.
|
|
Graphs of odd functions are
symmetric about the origin that is, such functions change
the sign but not absolute value when the sign of the independent variable is
changed, so that f
(x)
=
-
f (-x).
|
|
That
is, change of the sign of the independent variable of a function
reflects the graph of the function about the y-axis,
while change of the sign of a function reflects the graph of the
function about the x-axis.
|
|
The
graphs of
the translated cubic functions are symmetric about its
point of inflection.
|
|
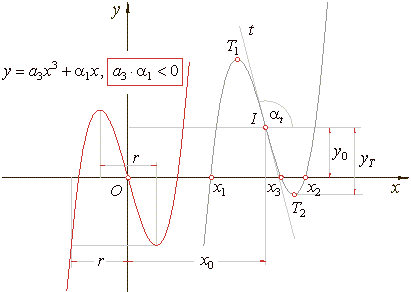
There are three types
(shapes) of cubic
functions whose graphs of the source functions are shown in the figure below:
|
|
|
y
=
a3x3
+ a2x2
+ a1x
+ a0 or y
-
y0
= a3(x
-
x0)3,
-
a22
+ 3a3a1
= 0 or a1
= 0.
|
|
therefore,
its source function y
=
a3x3,
and the tangent line through the point of
inflection is horizontal.
|
|
|
y
=
a3x3
+ a2x2
+ a1x
+ a0 or y
-
y0
= a3(x
-
x0)3
+
a1(x
-
x0)
where, a3a1>
0
|
|
and whose
slope of the tangent line through the point of inflection is
positive and equals a1.
|
|
|
y
=
a3x3
+ a2x2
+ a1x
+ a0 or y
-
y0
= a3(x
-
x0)3
+
a1(x
-
x0)
where, a3a1<
0
|
|
whose
slope of the tangent line through the point of inflection is
negative and is equal a1.
|
| The
graph of the source function type
2/2 has three zeros or roots at |
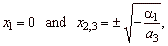 |
|
| and two turning
points at |
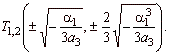 |
|
|
The
graphs
of the source cubic functions - the classification criteria
diagram
|
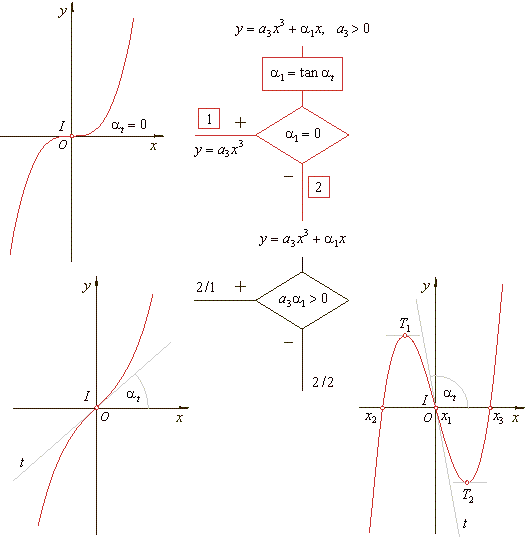
|
|
Translated
cubic functions
|
|
|
y
=
a3x3
+ a2x2
+ a1x
+ a0
or y
-
y0
= a3(x
-
x0)3,
-
a22
+ 3a3a1
= 0 and where
|
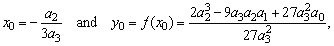
|
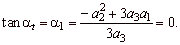 |
|
The
root
|
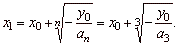 |
|
| The point of inflection
I(x0,
y0). |
|
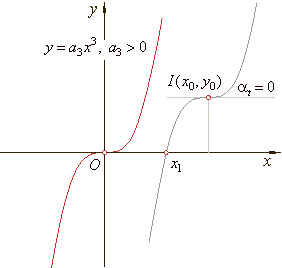 |
|
|
|
y
=
a3x3
+ a2x2
+ a1x
+ a0 or y
-
y0
= a3(x
-
x0)3
+
a1(x
-
x0)
where, a3a1>
0
|
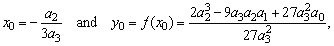
|
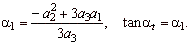 |
| The point of inflection
I(x0,
y0). |
|
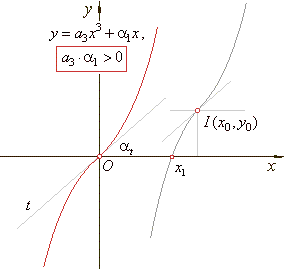 |
|
|
The
root
|
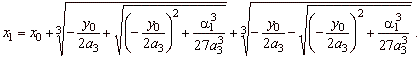
|
|
|
y
=
a3x3
+ a2x2
+ a1x
+ a0 or y
-
y0
= a3(x
-
x0)3
+
a1(x
-
x0)
where a3a1<
0
|
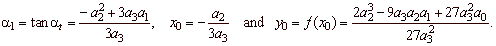
|
|
| If
| y0 | > | yT | |
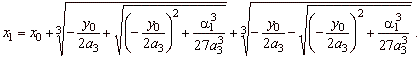 |
|
| If
| y0 | < | yT | |
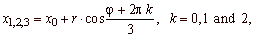 |
|
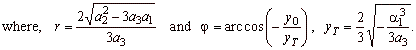
|
|
The turning points |
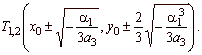 |
The point of inflection
I(x0,
y0). |
|
|
|
:: Drawing
a cubic function example
|
|
Example:
Given is cubic function y
=
(- 1/3)x3
-
4x2
- 12x
- 25/3,
find its source or original function and calculate the coordinates of translations, the zero
points, the turning points and the point of inflection. Draw
graphs of the source and the given cubic. |
| Solution:
1)
Let calculate the coordinates of translations,
|
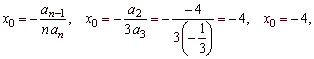 |
|
y0
= f
(x0),
y0
= f (-
4)
= (-1/3)
· (-
4)3 -
4 · (-
4)2
- 12
· (-
4)
- 25/3 =
-
3, y0
= -
3. |
| Therefore,
the point of inflection I
(-
4, -
3). |
| 2)
To
get the source cubic function we plug the coordinates
of translations (with changed signs) into the general
form
of cubic, |
| y
+ y0
=
a3(x
+
x0)3
+ a2(x
+
x0)2
+ a1(x
+
x0)
+ a0 thus, |
| y
-
3
= (-1/3)
·
(x
-
4)3
-
4(x
-
4)2
- 12(x
-
4)
- 25/3,
y
=
(-1/3)x3
+
4x
the
source function. |
| As, a3
< 0
and a3a1
< 0
given cubic is the type 2/2 whose graph is reflected around the x-axis. |
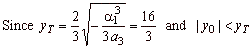 |
then, the function has three real
roots, |
|
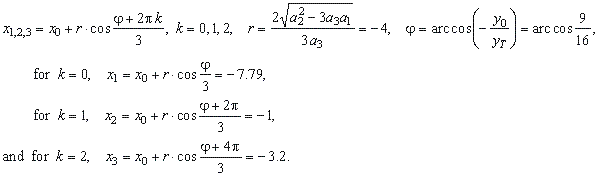 |
| By
plugging the coefficients of the source function and the
coordinates of translations
x0
and y0
into the above formula, we get the turning points, |
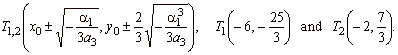 |
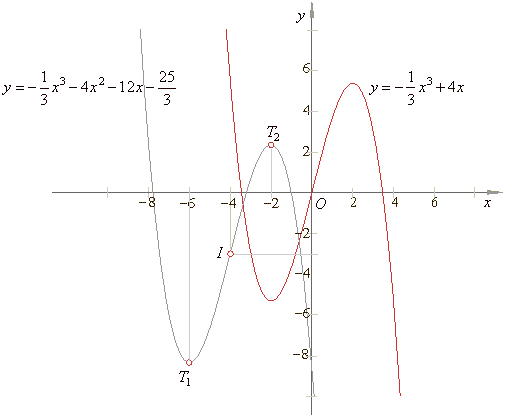 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Contents A
|
|
|
|
|

|
|
|
|
|
|
Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved.
|
|
|