|
|
|
|
ALGEBRA
|
|
|
|
::
Quartic
function, the fourth degree polynomial f
(x) = a4x4
+ a3x3 + a2x2
+ a1x + a0
|
|
Transformation of the quartic
polynomial from the general to the source form
|
|
To
get the source quartic function we plug the coordinates
of translations,
|
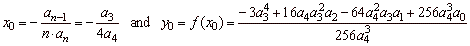
|
|
(with changed signs)
into general form of the quartic polynomial,
|
|
y
+ y0
= a4(x
+ x0)4
+
a3(x
+ x0)3
+
a2(x
+ x0)2
+
a1(x
+ x0) +
a0,
|
|
after
expanding and reducing obtained is the source
quartic function
|
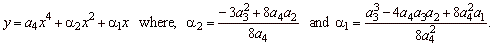
|
|
The
basic classification criteria applied to the source quartic
polynomial shows the diagram
|
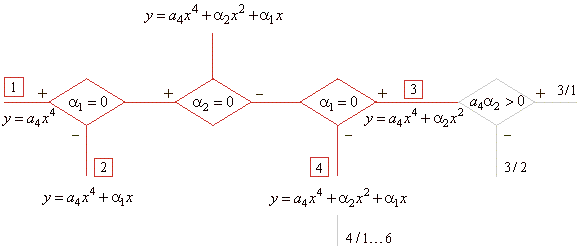
|
|
Thus, there are
ten types (different shapes of graphs) of quartic functions.
Applying additional criteria defined are the conditions
remaining six types of the quartic polynomial functions to
appear.
|
|
Observe that the
basic criteria of the classification separates even and odd nth
degree polynomials called the power functions or monomials as the first
type, since all coefficients a
of the source function vanish, (see the above diagram).
|
|
Therefore, the first type of
the qurtic polynomial
|
|
|
y
= a4x4
+ a3x3
+
a2x2
+
a1x + a0
or y
-
y0
=
a4(x
-
x0)4,
a2
= 0 and a1
=
0. |
|
|
| If
a4
·
y0
<
0
then
the roots are |
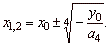 |
The turning point T(x0
, y0
).
|
|
|
|
|
:: Graph
of the power function - translated power or monomial functions
|
|
Thus, we
write the
translated
power function
or the polynomial of the first type,
|
|
y
- y0
= an(x
- x0)n,
|
|
where x0
= -
an
-
1/(n·an),
y0
=
f
(x0)
and n
is an even or
an odd positive integer.
|
| For
n
= 2m, m Î
N the even
power function has |
|
the turning point T
(x0,
y0). |
| The real
roots, |
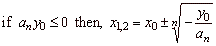 |
| as
shows the right figure (where an
> 0 ). |
|
|
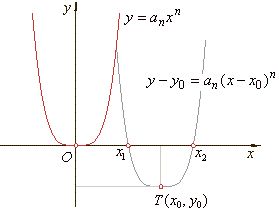 |
|
| For
n
= 2m + 1, m Î
N the odd power function |
|
has,
the point of inflection I
(x0,
y0),
at
=
0. |
| The real
root, |
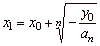 |
| as
shows the right figure (where an
> 0 ). |
|
|
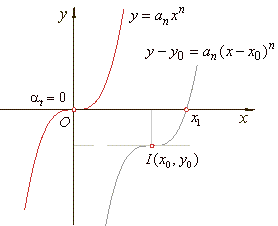 |
|
|
|
:: Drawing translated power or monomial
function example
|
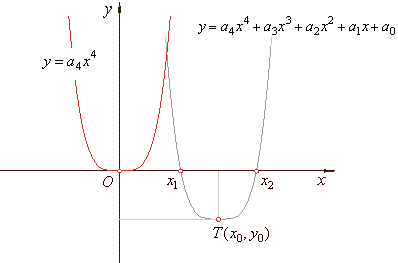
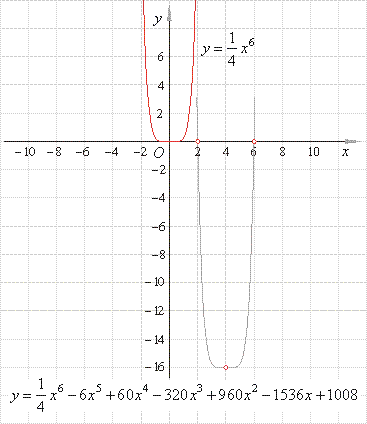
| Example:
Given sextic
polynomial y
= (1/4)x6 -
6x5
+
60x4
-
320x3
+
960x2
-
1536x
+
1008, |
|
find its source or original function and calculate
the coordinates of translations, the zero points and the turning
point. Draw
graphs of the source and the given sextic function. |
| Solution:
1)
Calculate the coordinates of translations,
|
| x0
= -
an
-
1/(n·an)
= -
a5/(6·a6)
= 4, x0
= 4
and y0
= f
(x0)
= -
16. |
| 2)
To get the source function, plug x0
and y0
with changed signs, into the general form of the sextic |
| y
+
y0
= a6(x
+
x0)6
+
a5(x
+
x0)5
+
a4(x
+
x0)4
+
a3(x
+ x0)3
+
a2(x
+ x0)2
+
a1(x
+ x0)
+
a0 |
| after
expanding and reducing we get, y
= (1/4)
x6 its
source function. |
| 3)
Inversely, by plugging the coordinates of translations into
the source function |
| y
- y0
= a6(x
- x0)6
or
y
- 16
= (1/4)(x -
4)6 |
| that,
after expanding yields given sextic polynomial. |
| As
the translated monomial or power function has zeros or roots, if
a6
· y0
<
0 then, |
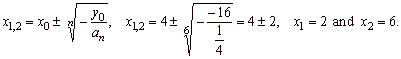 |
| The only turning point is
T(x0, y0)
or T(
4, -
16). |
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Contents A
|
|
|
|
|

|
|
|
|
|
|
Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved.
|
|
|