|
|
|
|
ALGEBRA
|
|
|
|
Polynomial
functions' properties
|
|
Every
polynomial has its initial position at the origin of the
coordinate system. A polynomial function written in
general form represents translation of its source
(original) function
|
|
fs(x)
= anxn
+ an
-
2
xn
-
2
+ an
-
3
xn
-
3
+
. . . +
a3x3
+
a2x2
+ a1x,
|
| in the direction of the
coordinate axes, where the coordinates of translations
are
|
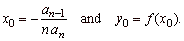
|
| Therefore,
each polynomial missing second term (an
-
1
=
0),
represents a source polynomial function whose graph is
translated in the direction of the y-axis
by y0
= a0.
|
| 1)
By plugging the coordinates of translations with changed
signs into a given polynomial y
= f
(x), expressed in the general form,
i.e.,
|
| y
+ y0
= an(x
+ x0)n
+ an
-
1(x
+ x0)n
-
1
+
. . . +
a2(x
+ x0)2
+
a1(x
+ x0)
+ a0
|
| and after expanding and reducing the above expression we get
its source function fs(x).
|
| 2)
Inversely,
by plugging the coordinates of translations into the
source polynomial function, i.e.,
|
| y
- y0
= an(x
- x0)n
+ an
-
2(x
- x0)n
-
2
+
. . . +
a2(x
- x0)2
+ a1(x
- x0),
|
| and after
expanding and reducing the above expression, we get given polynomial
f (x).
|
| Moreover, the
coefficients a
of the source polynomial are related to
corresponding value of the derivative of the given polynomial at x0,
like coefficients
of the Taylor polynomial in Taylor's or Maclaurin's formula,
|
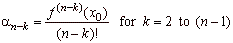
|
| where,
an
= an,
an
-
1
= 0,
a0
= f
(x0),
and f
(n
-
k)(x0)
denotes the (n
- k)-th
derivative at x0.
|
|
:: Sigma
notation of the polynomial function |
| Sigma
notation of the polynomial, where the coefficients a
of its source function are given by a recursive formula, |
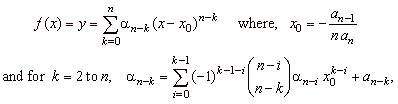 |
| while,
for k
= 0, an
= an,
for k
= 1, an-1
= 0
and for k
= n, a0
= f
(x0)
= y0. |
|
|
| Graphs of polynomial functions
|
| Polynomial
functions are named in accordance to their degree.
|
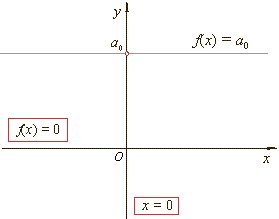
| ::
Zero polynomial
f
(x)
= 0 |
| The
constant polynomial f
(x)
= 0
is called the zero polynomial and
is graphically represented by the x-axis. |
| ::
Constant function
f (x)
= a0 |
| A
polynomial of degree 0, f
(x)
= a0,
is called a constant function,
its
graph is a horizontal line with the y-intercept
a0. |
|
 |
|
|
::
Linear
function, the first degree polynomial f
(x)
= a1x + a0
|
|
y
= a1
x + a0
or y
= m
x + c |
|
or y
= a1(x
-
x0)
or y
-
y0
= a1x,
|
|
where
x0
=
-
a0 /a1
and/or y0
= a0
are the x-intercept
and the y-intercept
respectively, and where the slope of the
line a1
=
m,
|
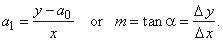 |
| By
setting x0
= 0 or y0
= 0
obtained is |
| the
source linear function,
y
= a1x. |
|
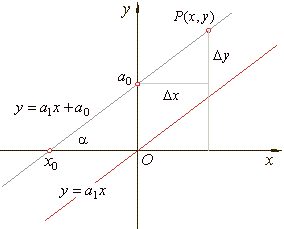 |
|
|
::
The roots of a
polynomial or zero function
values, x-intercepts
|
| A
zero of a function is a value of the argument (of a function) at
which the value of the function is zero. |
| Therefore,
zeros are values of the argument x
that satisfy or solve the equation f
(x)
= 0
or y
= 0. |
| The
zeros (roots) of a function correspond to the x-intercepts
of the graph. |
| An
x-intercept
is the point (x,
0)
where the graph of the function touches or crosses the x-axis. |
|
|
::
Linear
equation
|
| Thus, the
solution of the equation f
(x)
= 0
or y
= 0,
that
is |
| a1
x + a0
= 0
or m
x + c
= 0, |
| is the
zero of the linear function, the x-intercept or
the root of the first degree polynomial |
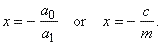 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Contents A
|
|
|
|
|

|
|
|
|
|
|
Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved.
|
|
|