|
| Trigonometry |
|
|
Trigonometric
Equations |
 The
Equations,
sin
(bx + c) = m, -1
<
m <
1,
cos
(bx + c) = m,
-1
<
m <
1,
The
Equations,
sin
(bx + c) = m, -1
<
m <
1,
cos
(bx + c) = m,
-1
<
m <
1,
|
|
tan
(bx
+ c) = m and cot
(bx
+ c) = m,
where
b,
c and
m are real
numbers. |
|
The
Equation
tan
(bx
+ c) = m, example |
|
The
Equation
cot
(bx
+ c) = m, example |
|
|
|
|
|
|
|
| The Equations,
sin
(bx + c) = m, -1
<
m <
1,
cos
(bx + c) = m, -1
<
m <
1, |
|
tan
(bx
+ c) = m and cot
(bx
+ c) = m,
where
b,
c
and m
are real numbers. |
| The given equations can be written as F
(bx +
c) = m
where F
substitutes a trigonometric function, x
is an arc
to be calculated and m
is a value of a given trigonometric function. |
| To every trigonometric function we can determine an arc,
a +
k · P
of which function value equals
m
that is F
(a +
k · P) = m,
where a
= x0
is the basic solution, and P
is the period, then |
| F(bx +
c) = F(a +
k · P)
or bx +
c = a +
k · P,
thus |
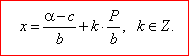 |
| Thus, from obtained general solution we can write a common solutions for every given
equation, |
 |
|
| The Equation
tan
(bx
+ c) = m example |
|
Example: Solve
the equation, |
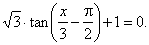 |
|
|
Solution: Rewrite
the equation to the form tan
(bx + c) = m,
|
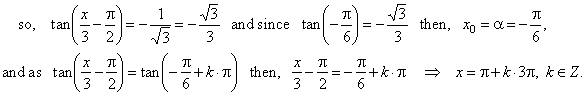 |
| We obtain the same result if we put given parameters,
b,
c, and corresponding basic solution |
| x0
= a
= tan-1
m to the common
solution that is, b
= 1/3,
c = -
p/2 and
x0
= a
= tan-1(-Ö3/3) =
-
p/6 |
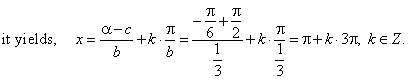 |
|
| The Equation
cot
(bx
+ c) = m example |
|
Example: Find
the solutions of the equation, cot
(-
2x + 10°) -
1 = 0.
|
|
Solution: Rearrange
the given equation to the form cot
(bx + c) = m, thus
cot (-
2x + 10°) = 1,
|
|
or cot
[-
(2x -
10°)] = 1
and since cot
(-
a)
= -
cot a
then, cot
(2x -
10°) = -
1, |
| and
cot (2x
-
10°) = cot (135° + k · 180°),
2x -
10° = 135° + k · 180° => x = 72°30′ +
k · 90°. |
| The general solution of the equation we get direct substituting the basic solution
x0
= a
and the constant b and
c
to the common solution, b
= 2,
c = -
10° and
x0
= a
= cot-1(-1) =
135°
give |
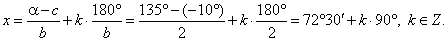 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Trigonometry
contents B |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |