|
| Trigonometry |
|
|
Trigonometric
Equations |
The
Equations,
sin
(bx + c) = m, -1
<
m <
1,
cos
(bx + c) = m,
-1
<
m <
1,
|
|
tan
(bx
+ c) = m and cot
(bx
+ c) = m,
where
b,
c and
m are real
numbers. |
|
The
Equation
sin
(bx + c) = m, -1
<
m <
1, example |
|
The
Equation
cos
(bx + c) = m,
-1
<
m <
1, example |
|
|
|
|
|
|
|
| The Equations,
sin
(bx + c) = m, -1
<
m <
1,
cos
(bx + c) = m, -1
<
m <
1, |
|
tan
(bx
+ c) = m and cot
(bx
+ c) = m,
where
b,
c
and m
are real numbers. |
| The given equations can be written as F(bx +
c) = m
where F
substitutes a trigonometric function, x
is an arc
to be calculated and m
is a value of a given trigonometric function. |
| To every trigonometric function we can determine an arc,
a +
k · P
of which function value equals
m
that is F(a +
k · P) = m,
where a
= x0
is the basic solution, and P
is the period, then |
| F(bx +
c) = F(a +
k · P)
or bx +
c = a +
k · P,
thus |
 |
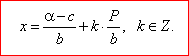| Thus, from obtained general solution we can write a common solutions for every given
equation, |
 |
|
| The Equation
sin
(bx + c) = m, -1
<
m <
1, example |
|
Example: Solve
the equation, |
 |
|
|
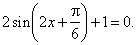Solution: Rewrite
the equation to the form sin
(bx + c) = m, so
sin
(2x + p/6)
= -
1/2
|
 |
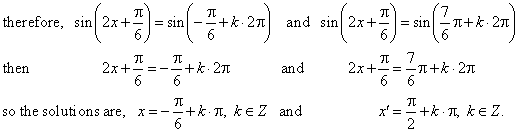| An alternative but similar solution can be obtained by substituting the values of,
b,
c
and m,
into |
| x0
= a
and x′0
= p
-
a
and to the common solution
written above |
 |
|
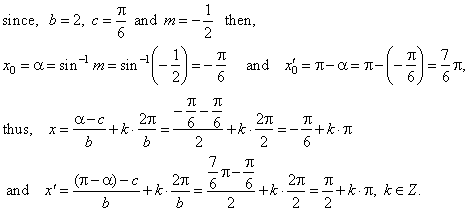| The Equation
cos
(bx + c) = m,
-1
<
m <
1, example |
|
Example: Find
the solutions of the equation, 2cos
(4x -
30°) + Ö3
= 0.
|
|
Solution: Rewrite
the equation to the form cos
(bx + c) = m, that
is cos
(4 x -
30°) = -
Ö3/2
it
follows that cos
(4 x -
30°)
= cos (+ 150° +
k · 360°)
|
|
and
4 x -
30°
= + 150° +
k · 360° |
|
so,
x = 45° +
k · 90°
and x′ = -
30° +
k · 90°, kÎ
Z. |
|
The same results we get by substituting the values, b
= 4, c = -
30°
and m =
-
Ö3/2,
into |
| x0
= a
= cos-1
m
= cos-1
(-
Ö3/2)
= 150° and
x′0
=
-
a
= -150° |
| then,
using the common solution formulas obtained are |
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
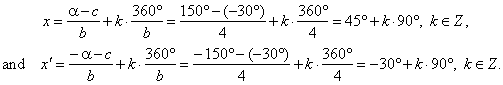| Trigonometry
contents B |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
