|
|
| ALGEBRA
- solved problems |
|
|
|
|
|
|
|
|
The
limit of a function
|
| Limits of
rational
functions |
| A
rational function is the ratio of two polynomial functions |
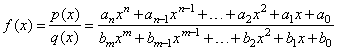 |
| where
n and m
define the degree of the numerator and the denominator
respectively. |
|
| Evaluating
the limit of a rational function at infinity |
| To
evaluate the limit of a rational function at infinity
we divide both the numerator and the denominator of
the function by the highest
power of x
of
the denominator. |
|
|
|
|
Evaluate
the limit |
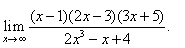 |
|
|
| Solution:
|
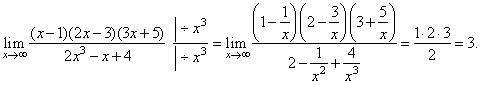 |
|
|
|
|
|
Evaluate
the limit |
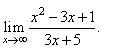 |
|
|
| Solution:
|
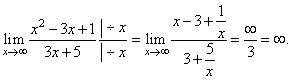 |
|
|
|
|
|
Evaluate
the limit |
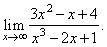 |
|
|
| Solution:
|
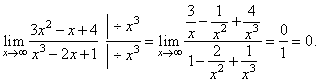 |
|
|
|
|
Evaluating
the limit of a rational function at a point
|
|
a)
The limit of a rational function that is defined at the given point
|
|
|
|
|
Evaluate
the limit |
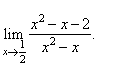 |
|
|
| Solution:
We first factor
the numerator and denominator |
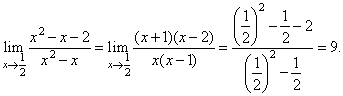 |
| Since
q(1/2) is
not
0
then |
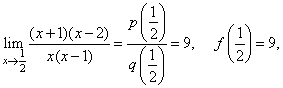 |
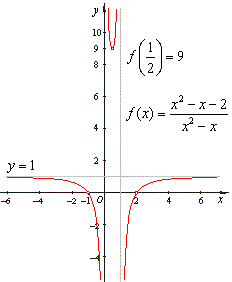
| x
= 0
and x
= 1
are vertical asymptotes, and y
= 1
is the |
| horizontal
asymptote, as is shown in the right figure. |
|
 |
|
|
|
|
b)
The limit of a rational function that is not defined at the
given point
|
|
|
|
|
Evaluate
the limit |
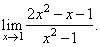 |
|
|
| Solution:
To avoid the indeterminate form 0/0,
the expression takes as x
®
1,
we factor and cancel common
factors |
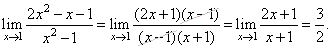 |
|
The rational function has the hole in the graph at x
= 1, |
| the vertical
asymptote
x
= -1
and
the horizontal |
| asymptote
y
= 2
since |
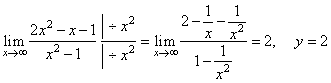 |
| as is shown in the right figure. |
|
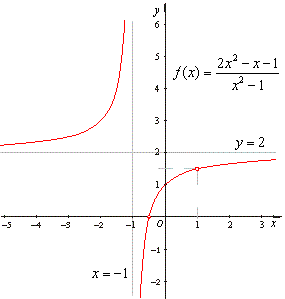 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Solved
problems contents - A |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |