ALGEBRA - solved problems
The limit of a function
The limit of a rational function at infinity containing roots (irrational expressions)
354.
   Evaluate the limit
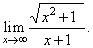Solution:  
355.
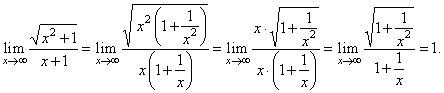   Evaluate the limit
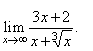Solution:  
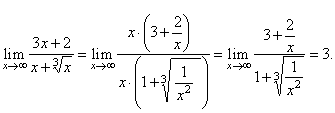The limit of a rational function at a point containing irrational expressions, use of substitution
Use of the method of substitution to avoid the indeterminate form of an expression.
356.
   Evaluate the limit
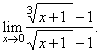Solution:   Let substitute,   x + 1 =  y6,   then as  x ® 0  then   y ® 1,   therefore
357.
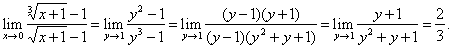
   Evaluate the limit
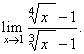Solution:   Let substitute,   x =  y12,   then as  x ® 1  then   y ® 1,   therefore
358.
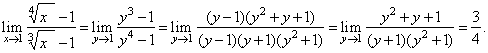
   Evaluate the limit
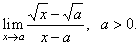Solution:   Let rationalize the numerator,
359.
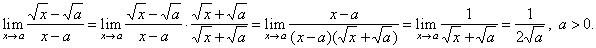
   Evaluate the limit
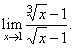Solution:   Let rationalize both the numerator and denominator,
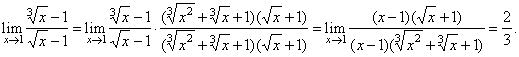
Evaluating trigonometric limits
We use the fundamental limit 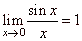and known trigonometric identities when solving trigonometric
limits.
360.
   Evaluate the limit
Solution:
361.
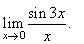   Evaluate the limit
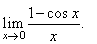Solution:   Since  cos(a + b) = cosacosb - sinasinb   then   cos2a = cos2a - sin2a = 1 - 2sin2a
that is    
362.
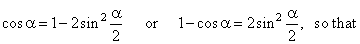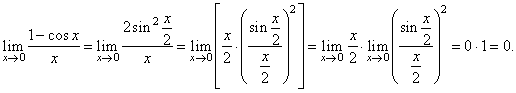
   Evaluate the limit
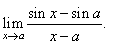Solution:   We use the sum to product identity and the fundamental trigonometric limit, thus
363.
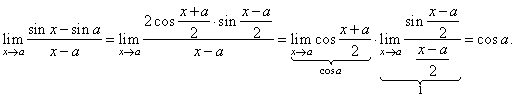
   Evaluate the limit
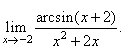Solution:   If we substitute  arcsin (x + 2) = t   then,
x + 2 = sin t  or  x = sin t - 2  so that,   t ® 0  as x ® -2,  therefore
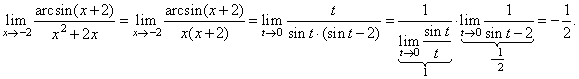
Solved problems contents - A
Copyright © 2004 - 2020, Nabla Ltd.  All rights reserved.