|
|
| ALGEBRA
- solved problems |
|
|
|
|
|
|
|
|
The
limit of a function
|
| Limits of
functions
properties |
| Assume that |
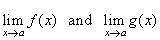 |
exist
and that c
is any constant. Then, |
|
|
|
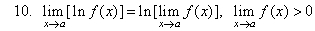 |
|
|
11.
Squeeze rule |
|
If f
(x)
< g (x) < h (x)
for all x
in an open interval that contains a,
except possibly at x
= a, |
|
and |
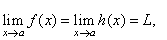 |
|
|
|
then |
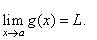 |
|
|
|
|
12.
Composition rule |
|
If f
(x)
is continuous at x
= b
and |
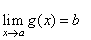 |
|
|
|
then, |
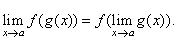 |
|
|
|
| Limits of
functions
properties use |
| Limits
that are commonly used are written below for easy reference, |
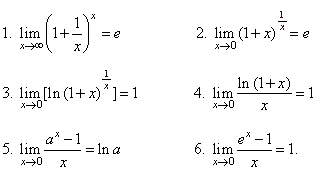 |
|
| By
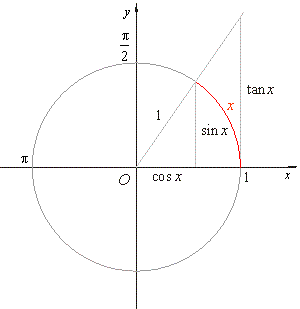
comparing the area of the sector of the arc x
with areas
of the two right triangles, the smaller triangle
with
legs sin x
and cos x,
and the bigger triangle with legs
tan x
and 1, shown on the right figure, we get |
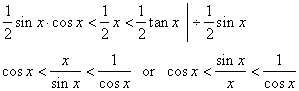 |
| Since
the left and the right side of the last
inequality tend
to the same limit 1, as x
tends to 0 then, applying
the squeeze rule obtained is |
|
|
|
 |
|
| the
fundamental or basic trigonometric limit.
Note
that the arc length x
is measured in radians. |
| Further, |
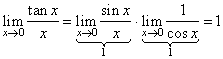 |
|
since both
factors on the right tend to 1, as x
tends to 0, then |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Solved
problems contents - A |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |