|
| Trigonometry |
|
|
|
|
|
Trigonometric
Functions |
 Unit of measurement of
angles - a radian (the circular measure)
Unit of measurement of
angles - a radian (the circular measure) |
|
Protractor - an instrument for measuring angles |
|
Degrees to radians and radians to degrees conversion examples |
 The unit circle or
the trigonometric circle
The unit circle or
the trigonometric circle |
|
Division of the circumference of the unit circle to
the characteristic angles |
|
|
|
|
|
|
| Unit of measurement of
angles - a radian (the circular measure) |
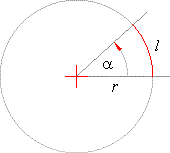
| The relation between
a central angle a
(the angle between two radii) and the corresponding arc l
in the circle of radius r is shown by the
proportion, |
| a°
: 360°
= l
: 2rp |
| It shows that the central angle
a°
compared to the round angle of 360° |
| (called
perigon) is in the same relation as the corresponding arc
l |
| compared
to the circumference 2rp.
Therefore, |
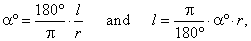 |
|
 |
|
| where the ratio |
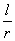 |
we call the
circular measure, usually denoted
arad,
i.e., |
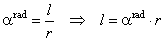 |
|
| thus, |
 |
|
|
The central angle subtended by the arc equal in length to the radius, i.e.
l = r, |
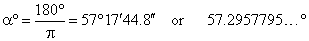 |
| we call it
radian. |
| Thus, the angle
a = 1° equals in
radians, |
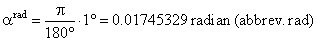 |
|
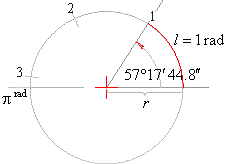 |
|
| or
arc1° =
0.01745329. Arc is abbreviation from Latin
arcus,
(p =
3.1415926535...). |
|
| Protractor
- an instrument for measuring angles |
| Mentioned relations between units of
measurement of an angle and arc clearly shows the protractor
shown in the
below figure marked with radial lines indicating degrees,
radians and
rarely used gradians (the angle of an entire
circle or round angle is 400 gradians). |
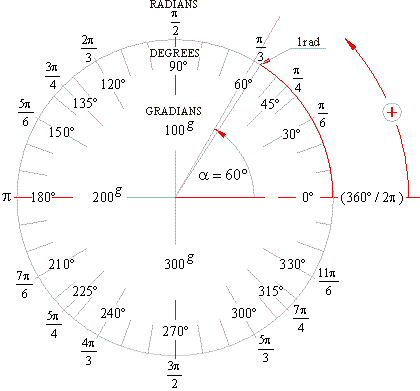 |
| A right angle
equals 100 grad (gradians). |
| The hundredth part of a right angle is
1g
grad,
and one 100th part of 1grad is centesimal arc minute 1c,
and one 100th part of centesimal arc
minute is centesimal arc second 1cc,
therefore |
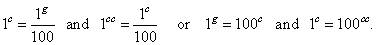 |
|
| Degrees
to radians and radians to degrees conversion examples |
| Example:
Convert
67°18´ 45" to radians.
|
| Solution: The given angle we write in the expanded notation and calculate its decimal
equivalent, |
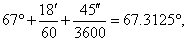 |
| then use the formula to convert degrees to radians |
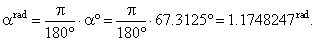 |
| Using a scientific calculator, the given conversion can be performed almost direct. |
| Before a calculation
choose right angular measurement (DEG, RAD, GRAD) by pressing
DRG key, then |
|
input, 67.1845
INV ®DEG 67.3125° |
| Because a calculator must use
degrees divided into its decimal part one should press ®DEG
(or ®DD) to get
decimal degrees. Then press
INV DRG® to get
radians, 1.174824753rad. |
|
| Example:
Convert 2.785rad
to degrees, minutes and seconds. |
| Solution: Using formula, |
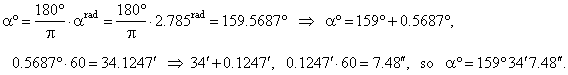 |
| The same result one obtains with a calculator through the
procedure, press DRG key to set RAD measurement,
then input 2.785
INV DRG® 177.2986066
grad = 177g29c86cc, press
again INV DRG®
159.5687459° obtained are
decimal degrees (DEG), and to convert to degrees/minutes/seconds press
INV ®DMS to
get 159° 34´
7.48". |
|
| Example:
Find the length of the
arc l
that subtends the central angle a
= 123°38´ 27"
in the circle of
radius r =
15 cm. |
| Solution: First express the angle
a
in decimal degrees, i.e. |
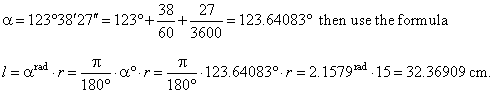 |
|
| The unit circle or
trigonometric circle |
|
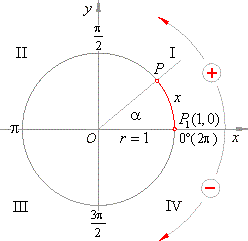
A circle of radius r =
1, with the center at the origin
O(0, 0) of a coordinate system, we call the
unit or trigonometric
circle, see the figure below. |
| The arc of the unit circle that describes a point traveling
anticlockwise
(by convention, clockwise is taken to be negative direction) from the initial position
P1(1,
0) on the x-axis, along
the circumference, to the terminal position P
equals the angular measure/distance x
= arad,
in radians.
|
| An angle is in standard position if its initial side lies along the
|
| positive
x-axis. |
|
If we take the positive direction of the x-axis as the beginning
|
| of a measurement of an angle (i.e.,
a
= 0rad,
both sides of
|
| an angle lie on the
x-axis), and the unit point
P1
as the initial
|
| point of measuring the arc, then the terminal side of an angle,
|
| which passes through the terminal point
P
of the arc,
|
|
rotating around the origin
(in any direction) describes different |
| angles,
and the terminal point P
corresponding arcs, |
| x
= arad
+ k · 2p,
k
= 0,
±1,
±2,
±3,
. . . |
| or
x
= a°
+ k · 360°, k
Î
Z. |
|
 |
|
|
It means that every arc x
ends in the same point P
in which ends the corresponding arc
a.
|
| Thus, at any
point P
on the circumference of the unit circle end infinite arcs
x = a
+ k ·
2p,
which differ by the
multiplier
2p, and any number
x associates only one point
P. |
|
| Division of the circumference of the unit circle to
the characteristic angles |
| There
is a common division of the circumference of the unit circle to
the characteristic angles or the corresponding
arcs which are the multipliers of the angles, 30°
(p/
6) and 45°
(p/
4). |
 |
|
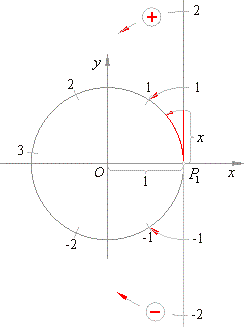
We can say that a unit circle is at the same time |
| numerical
circle. |
|
The numerical circle shown in the right figure is formed
|
| by winding the positive part of number line, with the unit |
| that equals the radius,
around the unit circle in the |
| anticlockwise
direction and its
negative part in clockwise |
| direction. |
|
| Therefore, the terms angle, arc and number in the
|
| trigonometric
definitions and expressions are mutually
|
| interchangeable.
|
|
 |
|
|
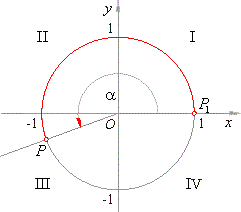
| Example:
In which quadrant lies second or the terminal side
of the angle x
= 1280°. |
| Solution: Dividing the given angle by
360°
we calculate the |
|
number of rotations, or round angles, described by terminal
side |
| of the angle x, and the remaining angle
a° position of
which we |
| want to find. |
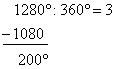 |
| since
x
= a°
+ k · 360°
then
k = 3
and a
= 200°. |
| therefore, terminal side of the angle
x lies in the third quadrant. |
|
 |
|
|
| Example:
In which quadrant lies the endpoint of the arc
x
= -
47p/3
of a unit circle. |
| Solution: Given
arc |
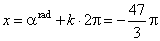 |
|
| can be expanded to |
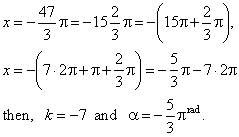 |
|
 |
|
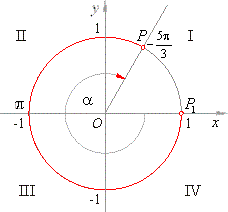
| Thus, the endpoint of the arc
x
moved around a unit circle in the clockwise (negative) direction 7 times and described additional arc
a
= -
(5/3)prad,
so its endpoint P
lies in the first quadrant. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Pre-calculus
contents C |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
|
|