|
|
|
|
Parametric Equations |
Parametric
equations definition |
|
Use
of parametric equations, example |
|
|
|
|
|
|
| Parametric
equations definition |
| When
Cartesian coordinates of a curve or a surface are represented as
functions of the same variable (usually written t),
they are
called the parametric equations. |
| Thus,
parametric equations in the xy-plane |
| x
= x (t)
and y
= y (t) |
| denote
the x
and y
coordinate of the graph of a curve in the plane. |
|
| The parametric equations of a line
|
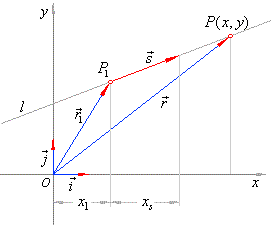
| If
in a coordinate plane a line is defined by the point P1(x1,
y1) and the
direction vector s
then, the position or (radius)
vector r
of any point P(x,
y) of the line |
| r
= r1 + t · s,
-
oo
< t < + oo
and
where, r1
= x1i + y1 j
and s
= xsi + ys j, |
| represents the vector equation of the line. |
| Therefore,
any point of the line can be reached by the |
| radius vector |
| r
= xi + y j
= (x1 + xst) i
+ (y1 + yst) j |
| since the scalar quantity t
(called the
parameter) can take any real value from -
oo
to + oo. |
| By
writing the scalar components of the above vector |
| equation obtained is |
| x
= x1 + xs · t |
| y
= y1 + ys · t |
|
|
| the parametric
equations of the line. |
|
 |
|
| To
convert the parametric equations into the Cartesian coordinates solve
given equations for t.
So |
 |
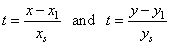| by
equating |
 |
|
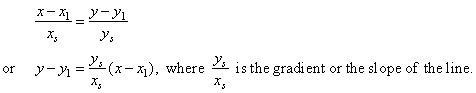| Therefore,
the parametric equations of a line passing through
two points P1(x1,
y1) and P2(x2,
y2) |
| x
= x1 + (x2 -
x1) t |
| y
= y1 + (y2 -
y1) t |
|
|
|
| Use
of parametric equations, example |
| Intersection point of a line and a plane
in three dimensional space
|
| The point of intersection is a common point of a line and a plane. Therefore, coordinates of intersection must
satisfy both equations, of the line l
and the plane P |
| |
 |
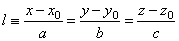and |
 |
|
|
|
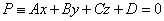where, (x0,
y0,
z0) is a
given point of the line and s =
ai + bj + ck
is direction vector of the line, and |
| N =
Ai + Bj + Ck
is the normal vector of the given plane. |
| Let
transform equation of the line into the parametric form |
 |
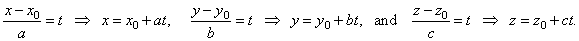| Then,
the parametric equation of a line, |
| x =
x0 + at,
y = y0
+ bt and z
= z0 + ct |
| represents coordinates of any point of
the line expressed as the function of a variable parameter t
which makes
possible to determine any point of the line according to a given condition. |
| Therefore, by plugging these variable coordinates of a point of the line into
the given plane determine what value
must have the parameter t,
this point to be the common point of the line and the plane. |
|
| Example:
Given is a line |
 |
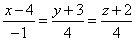and a plane
4x -
13y + 23z -
45 = 0, find the
|
|
| intersection
point of the line and the plane. |
| Solution: Transition from the symmetric to the parametric form
of the line
|
 |
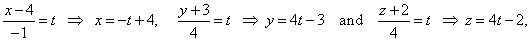| by plugging these variable coordinates
into the given plane we will find the value of the parameter t
such that these
coordinates represent common point of the line and the plane, thus |
| x =
-t +
4, y
= 4t -
3 and z
= 4t -
2 =>
4x -
13y + 23z -
45 = 0 |
| which
gives, 4 · (-t +
4) - 13 · (4t -
3) + 23 · (4t -
2) -
45 = 0 => t = 1. |
| Thus,
for t = 1
the point belongs to the line and the plane, so |
| x =
-t +
4 = -
1+ 4 = 3, y =
4t -
3 = 4 · 1 -
3 = 1 and z =
4t -
2 = 4 · 1 -
2 = 2. |
| Therefore, the intersection point
A(3,
1,
2) is the point which
belong to both, the line and the plane, prove. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Pre-calculus
contents C |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
