|
| Trigonometry |
|
|
|
|
|
Trigonometric
Functions |
 The unit circle or
the trigonometric circle
The unit circle or
the trigonometric circle |
|
Division of the circumference of the unit circle to
the characteristic angles |
|
|
|
|
|
|
| The unit circle or
trigonometric circle |
|
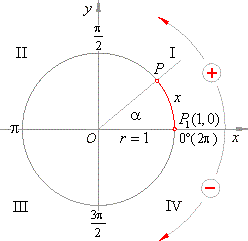
A circle of radius r =
1, with the center at the origin
O(0, 0) of a coordinate system, we call the
unit or trigonometric
circle, see the figure below. |
| The arc of the unit circle that describes a point traveling
anticlockwise
(by convention, clockwise is taken to be negative direction) from the initial position
P1(1,
0) on the x-axis, along
the circumference, to the terminal position P
equals the angular measure/distance x
= arad,
in radians.
|
| An angle is in standard position if its initial side lies along the
|
| positive
x-axis. |
|
If we take the positive direction of the x-axis as the beginning
|
| of a measurement of an angle (i.e.,
a
= 0rad,
both sides of
|
| an angle lie on the
x-axis), and the unit point
P1
as the initial
|
| point of measuring the arc, then the terminal side of an angle,
|
| which passes through the terminal point
P
of the arc,
|
|
rotating around the origin
(in any direction) describes different |
| angles,
and the terminal point P
corresponding arcs, |
| x
= arad
+ k · 2p,
k
= 0,
±1,
±2,
±3,
. . . |
| or
x
= a°
+ k · 360°, k
Î
Z. |
|
 |
|
|
It means that every arc x
ends in the same point P
in which ends the corresponding arc
a.
|
| Thus, at any
point P
on the circumference of the unit circle end infinite arcs
x = a
+ k ·
2p,
which differ by the
multiplier
2p, and any number
x associates only one point
P. |
|
| Division of the circumference of the unit circle to
the characteristic angles |
| There
is a common division of the circumference of the unit circle to
the characteristic angles or the corresponding
arcs which are the multipliers of the angles, 30°
(p/
6) and 45°
(p/
4). |
 |
|
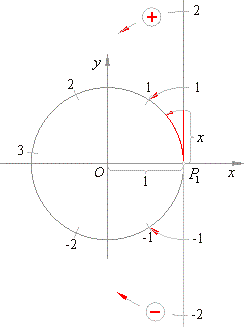
We can say that a unit circle is at the same time |
| numerical
circle. |
|
The numerical circle shown in the right figure is formed
|
| by winding the positive part of number line, with the unit |
| that equals the radius,
around the unit circle in the |
| anticlockwise
direction and its
negative part in clockwise |
| direction. |
|
| Therefore, the terms angle, arc and number in the
|
| trigonometric
definitions and expressions are mutually
|
| interchangeable.
|
|
 |
|
|
| Example:
In which quadrant lies second or the terminal side
of the angle x
= 1280°. |
| Solution: Dividing the given angle by
360°
we calculate the |
|
number of rotations, or round angles, described by terminal
side |
| of the angle x, and the remaining angle
a° position of
which we |
| want to find. |
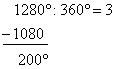 |
| since
x
= a°
+ k · 360°
then
k = 3
and a
= 200°. |
| therefore, terminal side of the angle
x lies in the third quadrant. |
|
 |
|
|
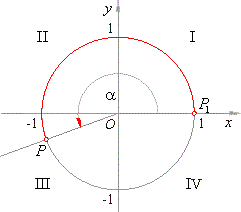
| Example:
In which quadrant lies the endpoint of the arc
x
= -
47p/3
of a unit circle. |
| Solution: Given
arc |
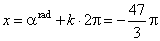 |
|
| can be expanded to |
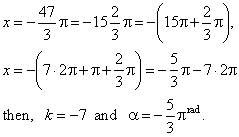 |
|
 |
|
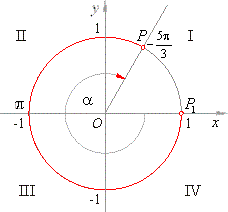
| Thus, the endpoint of the arc
x
moved around a unit circle in the clockwise (negative) direction 7 times and described additional arc
a
= -
(5/3)prad,
so its endpoint P
lies in the first quadrant. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Pre-calculus
contents C |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
|
|