|
| Trigonometry |
|
|
|
|
|
Trigonometric
Equations |
 Basic Trigonometric
Equations
Basic Trigonometric
Equations |
|
The
equation cos
x = a |
|
|
|
|
|
|
|
|
|
Trigonometric
equations
|
|
An equation that involves one or more trigonometric functions, of an unknown arc, angle or number, is called trigonometric equation.
|
|
Basic trigonometric
equations
|
|
The equation cos
x = a, -1
<
a <
1
|
|
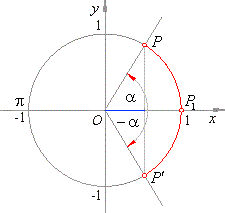
The solutions of the equation are arcs
x
whose function's value
of cosine equals a.
|
|
Infinite many arcs whose cosine value equals a end in points,
P |
|
and P′, that are |
| |
x
=
arad
+ k
·
2p
and x′
= - arad
+ k
·
2p,
k Î
Z. |
|
|
| This is the set of the general solutions of the given equation. |
| For
k = 0 follows the basic solutions of the equation |
| |
x0
=
arad
and x0′
= - arad.
|
|
|
|
 |
|
|
Therefore, if cos
x = a, -1
< a
<
1 then,
x = ± arad
+ k ·
2p
= + arccos a, k Î
Z.
|
|
For example if, a =
-1,
then, cos
x = -1
=> x = p
+ k
·
2p,
k Î
Z,
|
|
a = 0
cos x =
0 =>
x = p/2
+ k
·
p,
k Î
Z,
|
|
or a =
1
cos x =
1 =>
x = k
·
2p,
k Î
Z.
|
|
|
|
Since cosine function passes through all values from range
-1
to 1
while arc x
increases from 0
to p, one of the arcs from this interval must satisfy the equation
cos x = a.
|
|
This arc, denoted x0,
we call the
basic solution.
|
|
Thus, the basic solution of the equation
cos x = a,
-1
<
a
<
1
is the value of inverse cosine function,
|
|
x0
=
arccos a
or x0
= cos-1
a,
|
|
that is, an arc or angle (whose cosine equals
a) between
0
and p
which is called the principal
value.
|
|
Scientific calculators are equipped with the
arccos (or
cos-1) function which, for a given argument between
-1
and 1, outputs arc (in radians) or angle (in degrees) from the range
x0 Î
[0,
p].
|
|
|
|
Example: Solve
the equation, cos
x = -
0.5.
|
|
Solution: In the unit circle in
the below figure shown are the two arcs, of which cosine value equals
-
0.5, that represent the basic solutions of the given equation
|
|
x0
= 120°
or x0′ =
-120°
|
|
while the abscissas of the intersection points of the line
y = -
0.5 with the graph of cosine function represent
the set of the general solution
|
|
x
= +
120°
+ k
·
360°
or x
= +
2p/3
+ k
·
2p,
k Î
Z.
|
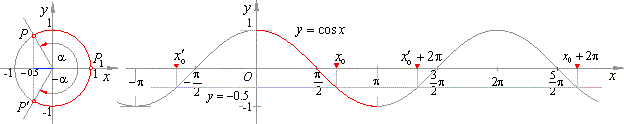
|
|
The same results we obtain by using calculator if we set DEG then input
|
|
-
0.5
INV cos
(or cos-1)
=> x0
= 120°
and x0′ =
-120° that
are the basic solutions.
|
|
Or we input the same while calculator is set in RAD mode to get the arc in radians that is
|
|
x0
= 2.094395102rad
= 2p/3rad.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Pre-calculus
contents G |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |