|
| Trigonometry |
|
|
|
|
|
Trigonometric
Equations |
 Basic Trigonometric
Equations
Basic Trigonometric
Equations |
|
The equation sin
x = a |
|
|
|
|
|
|
|
|
Trigonometric
equations
|
|
An equation that involves one or more trigonometric functions, of an unknown arc, angle or number, is called trigonometric equation.
|
|
|
|
Basic trigonometric
equations
|
|
The equation sin
x = a, -1
<
a <
1
|
|
To solve the equation we should find the arc x (or angle in radians) of which function value of sine equals a.
|
|
Infinite many arcs whose sine value equals
a
end in the points P
and P′
that is,
|
| x
=
arad
+ k
·
2p
= arcsin a
+ k
·
2p, k Î
Z,
and
|
| x′
= (p
- arad)
+ k
·
2p
= (p
- arcsin
a)
+ k
·
2p, k Î
Z,
|
|
|
| there are an infinite number of solutions obtained by giving
|
| different
integer values to
k. This is the set of the
general
|
| solutions of the
given trigonometric equation.
|
| For
k = 0 obtained
are, |
| x0
= arcsin a
and x0′
= p - arcsin a, |
|
or
x0
= sin-1
a
and x0′
= p - sin-1
a, |
|
|
| the
basic
solutions.
|
|
 |
|
|
The principal values of the inverse sine function,
arcsin or
sin-1,
are those between -
p/2 and
p/2.
|
|
The above solutions of the equation
sin x =
a, -1
<
a <
1 can concisely be written as
|
| |
x
= (-1)k
· arcsin a
+ k
·
p,
k Î
Z.
|
|
|
|
|
|
For example,
a) sin x
= -1,
b) sin
x
=
0,
c) sin
x
= 1,
|
|
x
= -
p/2
+ k ·
2p.
x
= k
·
p.
x
= p/2
+ k ·
2p, k Î
Z.
|
|
|
|
Using a scientific calculator to obtain principal (or basic) value of the inverse sine function, arcsine, input value
for
a
and press, sin-1
(or INV sin or 2nd sin).
|
|
Obtained is an arc (in radians) or angle (in degrees)
between -
p/2 and
p/2, depending on what measurement (DEG or
RAD) was set before, by the DRG key.
|
|
|
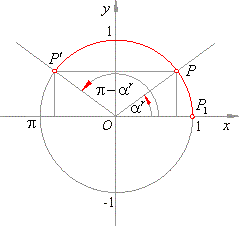
| Example: Solve
the equation, |
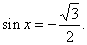 |
|
|
|
Solution: Let
first find the basic solutions of the equation.
We should remember values of the trigonometric
|
|
functions of some special arcs (angles) like
|
 |
|
|
Since the basic solutions for
sin x =
a are,
x0
=
arad
and x0′
= p -
arad,
then
|
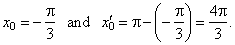
|
|
While from
x
= x0 + k
·
2p
and x′
= x0′
+ k
·
2p, k Î
Z,
follow
|
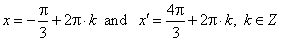
|
|
the general solution
of the given equation.
|
|
The basic solutions we see on the unit circle in
the below figure while from the graph can be seen that the line
y = -
Ö3/2
intersects the sine function at infinite many points whose abscissas represent the general solutions.
|
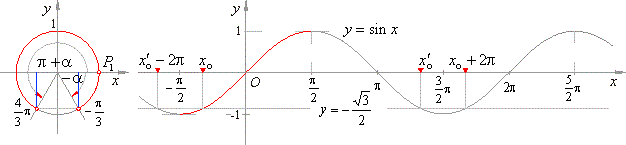
|
|
|
|
Example: Solve
the equation, sin x =
0.433266.
|
|
Solution: Find the basic solution using a calculator.
Press DRG key to set DEG, meaning degree measurement of the
corresponding angle, then input
|
|
0.433266 sin-1
(or INV sin) =>
x0 =
a° =
25.67500799° =
25°40′30″,
|
|
x0′ =
180° -
a° =
154.324992° =
154°19′30″.
|
|
To transform the decimal degrees to deg., min. and sec. form,
press ®
DMS.
|
|
If the basic solution should be presented in radians, set RAD measurement.
|
|
It is also possible an angle
expressed in degrees convert straight to radians. While display shows decimal degrees press DRG®
so obtained are,
|
|
x0 =
arad
=
0.448113424rad
and x0′ =
p
- arad =
2.693479229rad.
|
|
Thus, general solution presented by angles,
x
= x0 + k
·
360° =
25°40′30″
+ k
·
360°,
k Î
Z,
|
|
and x′
= x0′ +
k
·
360° =
154°19′30″ +
k
·
360°,
k Î
Z,
|
|
or by arcs, x
= x0 + k
·
2p =
0.448113424rad +
k
·
2p,
k Î
Z,
|
|
and x′
= x0′ +
k
·
2p =
2.693479229rad
+ k
·
2p,
k Î
Z.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Pre-calculus contents
G |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |