|
| Trigonometry |
|
|
|
|
Inverse Trigonometric Functions or
Arc-functions and their Graphs |
|
Inverse
functions
|
|
The
arc-sine function and the arc-cosine function |
|
The
arc-sine function |
|
The
arc-cosine function |
|
The
graph of the
arc-sine
function and the arc-cosine
function |
|
The
arc-tangent function and the
arc-cotangent function |
|
The
arc-tangent function |
|
The
arc-cotangent function |
|
The
graph of the
arc-tangent function and the
arc-cotangent function |
|
The
arc-cosecant function and the arc-secant function |
|
The
graph of the
arc-cosecant and the
arc-secant function |
|
|
|
|
|
|
| Inverse Trigonometric Functions or
Arc-functions and their Graphs |
| Inverse
functions
|
| The inverse function, usually written
f -1, is the function whose
domain and the range are respectively the range and domain of a given function
f, that is |
| f
-1(x)
= y if and only
if f
(y)
= x . |
| Thus, the
composition of the inverse function and the given function returns
x, which is called the
identity function,
i.e., |
| f
-1(ƒ(x))
= x
and f
(f
-1(x))
= x. |
| The inverse of a function undoes the procedure
(or function) of the given function. |
| A pair of inverse functions is in
inverse relation. |
| Example: If
given
f (x)
= log2 x
then f -1(x)
= 2x
since, |
 |
|
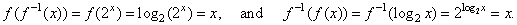| The
arc-sine function and the arc-cosine function |
|
- The
arc-sine function
y
= sin-1x
or y
= arcsin x
is the inverse of the sine function, so that its value for
any
argument is an arc (angle) whose sine equals the given argument. |
| That
is, y
= sin-1x
if and only if x
= sin y.
For
example, |
 |
|
|
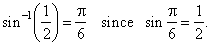Thus, the arc-sine
function is defined for arguments between -1
and 1, and its principal
values are by
convention taken to be those between -p/2
and p/2. |
|
|
- The
arc-cosine function
y
= cos-1x
or y
= arccos x
is the inverse of the cosine function, so that its
value for any
argument is an arc (angle) whose cosine equals the given
argument. |
| That
is, y
= cos-1x
if and only if x
= cos y.
For
example, |
 |
|
|
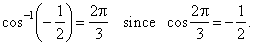Thus, the arc-cosine
function is defined for arguments between -1
and 1, and its principal
values are by
convention taken to be those between 0 and p. |
|
| The
graph of the
arc-sine
function and the arc-cosine
function |
|
|
|
| The
arc-tangent function and the
arc-cotangent function |
|
- The
arc-tangent function
y
= tan-1x
or y
= arctan x
is the inverse of the tangent function, so that its
value for any
argument is an arc (angle) whose tangent equals the given
argument. |
| That
is, y
= tan-1x
if and only if x
= tan
y.
For
example, |
 |
|
|
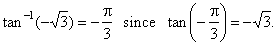Thus, the arc-tangent
function is defined for all real arguments, and its principal
values are by
convention taken to be those strictly between -p/2
and p/2. |
|
|
- The
arc-cotangent function
y
= cot-1x
or y
= arccot x
is the inverse of the cotangent function, so that
its value for any
argument is an arc (angle) whose cotangent equals the given
argument. |
| That
is, y
= cot-1x
if and only if x
= cot
y.
For
example, |
 |
|
|
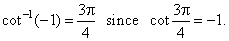Thus, the arc-cotangent
function is defined for all real arguments, and its principal
values are by
convention taken to be those strictly between 0
and p. |
|
| The
graph of the
arc-tangent function and the
arc-cotangent function |
|
|
|
| The
arc-cosecant function and the arc-secant function |
|
- The
arc-cosecant function
y
= csc-1x
or y
= arccsc x
is the inverse of the cosecant function, so that its
value for any
argument is an arc (angle) whose cosecant equals the given
argument. |
| That
is, y
= csc-1x
if and only if x
= csc
y.
For
example, |
 |
|
|
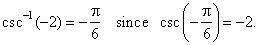Thus, the arc-cosecant
function is defined for arguments less than -1
or greater than 1, and its principal
values are by
convention taken to be those between -p/2
and p/2. |
|
|
- The
arc-secant function
y
= sec-1x
or y
= arcsec x
is the inverse of the secant function, so that its value for any
argument is an arc (angle) whose secant equals the given
argument. |
| That
is, y
= sec-1x
if and only if x
= sec
y.
For
example, |
 |
|
|
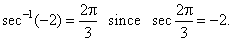Thus, the arc-secant
function is defined for arguments less than -1
or greater than 1, and its principal
values are by
convention taken to be those between 0
and p. |
|
| The
graph of the
arc-cosecant and the
arc-secant function |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Pre-calculus contents
G |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
