|
| Trigonometry |
|
|
Trigonometric
Equations |
 Equations of the Type
a
cos
x +
b
sin
x = c
Equations of the Type
a
cos
x +
b
sin
x = c |
|
Introducing new unknown
t
= tan x/2 |
|
Introducing new unknown
t
= tan x/2
example |
|
|
|
|
|
|
| Equations of the type
a
cos
x +
b
sin
x = c |
| To
solve the trigonometric equations which are linear in sin
x and cos
x, and where, a,
b,
and c
are real |
| numbers
we can use the two methods, |
| a)
introducing an auxiliary angle, and b)
introducing new unknown. |
|
|
Introducing new unknown t
= tan x/2 |
|
If in the equation a
cos x + b sin x = c
we substitute the sine and cosine functions by
tan x/2 = t
that is, |
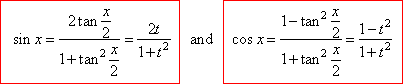 |
| the equation becomes |
 |
and after rearranging |
(a +
c) ·
t2
-
2b · t + (c -
a) = 0. |
|
|
Obtained quadratic equation will have real solutions
t1,2
if its discriminant is greater then or equal to
zero, |
|
that is if
(-2b)2
-
4 (a + c)(c -
a) >
0
or c2
< a2
+ b2,
which is earlier mentioned condition. |
| If this condition is satisfied, the solutions,
t1
and t2
can be substituted into tan x/2 =
t1 and
tan x/2 = t2. |
| Thus,
obtained are the basic trigonometric equations. |
|
| Introducing new unknown
t
= tan x/2
example |
|
Example: Solve the equation,
5 sin x
-
4 cos x = 3.
|
|
Solution: Given equation is of the form
a
cos x + b sin x = c
therefore parameters are,
a
= -
4, b =
5 and
|
| c
= 3, after introducing new unknown
tan x/2 = t
and substituting the values of the parameters into equation |
| (a +
c) ·
t2
-
2b · t + (c -
a) = 0
gives (-
4 + 3) ·
t2
-
2 · 5 · t + [3 - (-
4)] = 0 |
| or
t2
+ 10t -
7 = 0,
t1,2
= -
5 +
Ö25
+ 7 = -
5 +
4Ö2. |
|
Obtained values for variable
t
we plug into substitutions,
|
|
tan x/2 = t1,
x/2 = tan-1
(t1)
or x =
2arctan(-
5 -
4Ö2) |
|
x = 2 · (-
84°38′21″ + k · 180°) =
-
169°16′42″ + k · 360°,
|
|
tan x/2 = t2,
x/2 = tan-1
(t2)
or x′ =
2arctan(-
5 + 4Ö2) |
|
x′ =
2 · (33°17′56″ + k · 180°) =
66°35′53″ + k · 360°. |
| The same result we obtain using the method of introducing the auxiliary angle
j. Plug the given parameters
|
| a
= -
4, b =
5 and c
= 3 into tan
j
= b/a,
tan j =
5/(-
4) => j =
-51°20′24″,
cos j =
0.624695, |
| then
from the equation |
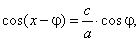 |
cos
(x + 51°20′24″) =
(3/-
4) · 0.624695 |
|
| |
|
or x
+ 51°20′24″ =
arccos [(3/-
4) · 0.624695], |
|
| thus,
x +
51°20′24″ =
+ 117°56′18″ + k · 360° => x =
+ 117°56′18″
-
51°20′24″ + k · 360°. |
|
|
Trigonometric equations of the form a
cos x + b sin x = c
we do not solve using the identity
|
 |
|
since that way given equation becomes quadratic with four solutions but only two of
them satisfy it. |
|
We will solve the equation from the previous example using this method anyway. |
|
|
Example: Solve the equation,
5 sin x
-
4 cos x = 3
by substituting |
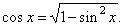 |
|
|
Solution: Squaring both sides of an equation may introduce extraneous
or redundant (not needed) solutions.
|
 |
| By plugging the results into given equation show that only solutions
b) and c) satisfy the equation what match with previous results obtained using another two methods.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Pre-calculus contents
G |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |