|
| Trigonometry |
|
|
|
|
|
Trigonometric
Equations |
 Basic Trigonometric
Equations
Basic Trigonometric
Equations |
|
The equation
tan
x = a |
|
The equation cot
x = a |
|
|
|
|
|
|
|
|
Trigonometric
equations
|
|
An equation that involves one or more trigonometric functions, of an unknown arc, angle or number, is called trigonometric equation.
|
|
|
|
Basic trigonometric
equations
|
|
The equation tan
x = a
|
|
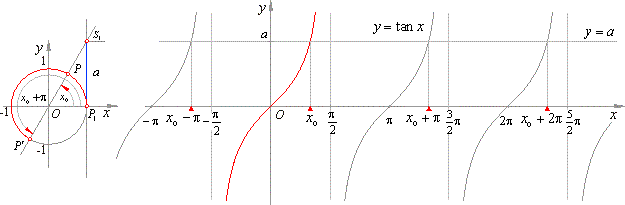
The solutions of the equation are the arcs of which the function value of tangent equals
a.
|
|
At the points, P and
P′,
of the unit circle, end infinite many arcs
|
| |
x
= x0 + k
·
p
= arad
+ k
·
p
= arctan a + k
·
p,
k Î
Z,
|
|
|
|
whose tangent values equals
a. These arcs represent the set of the
general solution (see the
figure below).
|
|
While the arc x
increases from -
p/2
to p/2
the function tangent passes through all the values from the
|
|
range (-
oo,
+ oo),
what means that the equation
tan x =
a will have its
basic solution within that interval.
|
|
| The basic solution
|
x0
= arctan a
or x0
= tan-1
a
|
|
|
|
|
|
Example: Solve
the equation, tan
x = -
2.
|
|
Solution: Set a calculator to DEG mode and input
|
|
-
2 and press
tan-1
(or INV tan)
key
=> x0
= -
63.43494882°
= -
63°26′06′′
|
|
obtained is the basic solution. To convert from decimal
degree to, deg., min., sec form, press ®DMS
key.
|
|
The general solution, x
= x0 + k
· 180°
=> x
= -
63°26′06′′ +
k
· 180°,
k Î
Z,
|
|
or in radians, x
= x0 + k
·
p
=> x
= -
1.107148718
+ k
·
p,
k Î
Z.
|
|
To convert from decimal
degree to radians change from DEG to RAD mode by pressing DRG®
key.
|
|
|
|
The equation cotx = a
|
|
The solutions of the equation are arcs
x
whose function value of cotangent equals
a.
|
|
At the points, P and
P′,
of the unit circle, end infinite many arcs
|
| |
x
= x0 + k
·
p
= arad
+ k
·
p
= arccot a + k
·
p,
k Î
Z,
|
|
|
|
whose cotangent equals
a.
These arcs represent the general
solution of the
equation cot
x = a.
|
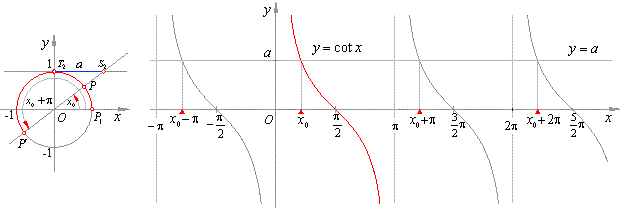
|
|
The cotangent function passes through all the values from the range
(-
oo,
+ oo)
while the arc x
increases from
0
to p.
|
|
Therefore, the equation
cot x
= a
will have its basic solution within that interval, as shows the
graph above.
|
| The basic solution
is
|
x0
=
arccot a
or x0
= cot-1
a
|
|
|
|
and we calculate it using tangent function that is,
|
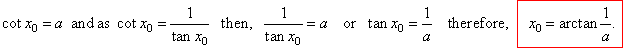
|
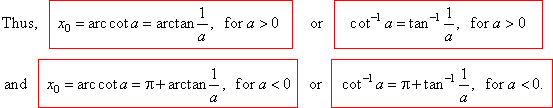
|
|
By adding p
to the formula for the negative a
we compensate the difference in the definitions of the tangent of the principal values of inverse, cotangent and tangent.
|
|
We also can calculate the basic solution using the known identity
tan (p/2
-
x0) =
cot x0.
|
|
By substituting cot
x0
= a
or x0 =
arccot a
then, tan
(p/2
-
x0) =
a
or p/2
-
x0 =
arctan a,
|
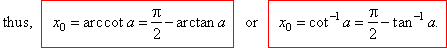
|
|
|
|
Example: Solve
the equation, cot
x = -
1.85.
|
|
Solution: The basic solution we calculate using formula
x0 =
p/2
-
arctan a
or x0 =
90°
-
arctan a.
|
|
Set a calculator to DEG mode and input
|
|
-
1.85
press tan-1
(or INV tan)
key
=> x0
= 90°
-
( -
61.60698058°
)
= 151°36′
25.13″,
|
|
and the general solution
x
= x0 + k ·
p
or x
= x0 +
k ·
180°
= 151°36′
25.13″ +
k ·
180°,
k Î
Z.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Pre-calculus
contents G |
|
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |