Geometric series - The sum of an infinite converging geometric series

Sequences and Series

Series

The sum of an infinite geometric sequence, infinite geometric series

Converting recurring decimals (infinite decimals) to fraction

The sum of an infinite geometric sequence, infinite geometric series

An infinite geometric series converges (has a finite sum even when n is infinitely large) only if the absolute ratio of successive terms is less than 1 that is, if -1 < r < 1.

The sum of an infinite geometric series can be calculated as the value that the finite sum formula takes (approaches) as number of terms n tends to infinity,

first rewrite S_n, into

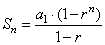so that

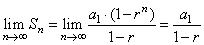since | r | < 1, then rⁿ ® 0 as n ® oo

thus,

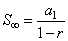the sum of an infinite converging geometric series.

Converting recurring decimals (infinite decimals) to fraction

Recurring or repeating decimal is a rational number (fraction) whose representation as a decimal contains a pattern of digits that repeats indefinitely after decimal point.

The decimals that start their recurring cycle immediately after the decimal point are called purely recurring decimals.

Purely recurring decimals convert to an irreducible fraction whose prime factors in the denominator can only be the prime numbers other than 2 or 5, i.e., the prime numbers from the sequence {3, 7, 11, 13,17, 19, . . }.

The decimals that have some extra digits before the repeating sequence of digits are called the mixed recurring decimals.

The repeating sequence may consist of just one digit or of any finite number of digits. The number of digits in the repeating pattern is called the period.

Mixed recurring decimals convert to an irreducible fraction whose denominator is a product of 2's and/or 5's besides the prime numbers from the sequence {3, 7, 11, 13,17, 19, . . . }.

All recurring decimals are infinite decimals.

Converting purely recurring decimals to fraction

Example: Convert the purely recurring decimal

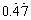to fraction.

Solution: Given decimal we can write as the sum of the infinite converging geometric series

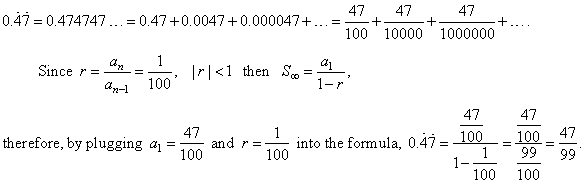Notice that, when converting a purely recurring decimal less than one to fraction, write the repeating digits to the numerator, and to the denominator of the equivalent fraction write as much 9's as is the number of digits in the repeating pattern.

Thus, for example:

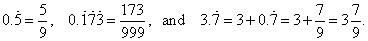Converting mixed recurring decimals to fraction

Example: Convert the mixed recurring decimal

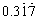to fraction.

Solution: Given decimal we can write as the sum of 0.3 and the infinite converging geometric series,

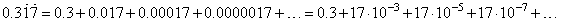Since the repeating pattern is the infinite converging geometric series whose ratio of successive terms is less than 1, i.e., r = 0.01 then we use the formula for the sum of the infinite geometric series S_oo = a₁ / (1 - r),

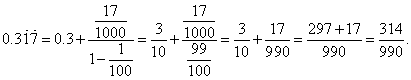Notice that, when converting the mixed recurring decimal less than one to fraction, write the difference between the number formed by the entire sequence of digits, including the digits of the recurring part, and the number formed only by the digits of the non-recurring pattern to its numerator. To the denominator of the equivalent fraction write as much 9’s as is the number of digits in the repeating pattern and add as much 0’s as is the number of digits in the non-recurring pattern.

Thus, for example:

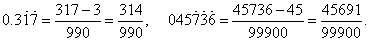Intermediate algebra contents