|
| Sequences and
Series
|
|
|
|
| Series
|
Geometric series
|
|
The sum of an infinite geometric
sequence, infinite geometric series |
|
The sum of an infinite converging
geometric series, examples
|
|
|
|
|
|
|
| The sum of an infinite geometric
sequence, infinite geometric series |
| An
infinite geometric series converges (has a finite sum even when n
is infinitely large) only
if the absolute ratio of successive terms is less than 1 that is,
if
-1
< r <
1. |
| The
sum of an infinite geometric series can be calculated as the value that
the finite sum formula takes (approaches) as number of terms n
tends to infinity, |
| first
rewrite
Sn,
into |
 |
|
|
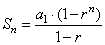| so
that |
 |
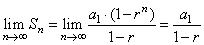since
| r
| < 1, then rn
®
0
as n
® oo |
|
| thus, |
 |
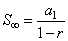the sum of an infinite converging
geometric series.
|
|
|
| The sum of an infinite converging
geometric series, examples
|
| Example:
Given a square with
side a.
Its side is the diagonal of the second square. The side of this square
is then the diagonal of the third square and so on, as shows the figure
below. Find the sum of areas of all these
squares. |
| Solution:
Using
the given conditions, |
|
|
 |
|
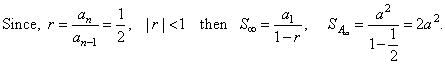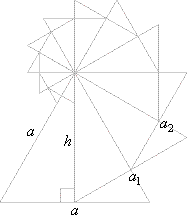
| Example:
Given an equilateral triangle with the side a.
Its height is the side of another equilateral triangle. The height of
this triangle is then the side of the third equilateral triangle and so
on, as shows the figure below. Find the sum of areas of all these
triangles. |
| Solution:
a1
= h, a2
= h1, a3
= h2,
and so on. Thus, |
 |
|
 |
|
 |
|
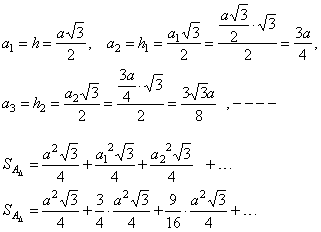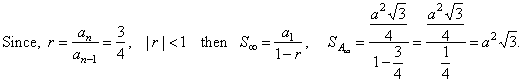| Example:
In a circle of the radius r
inscribed is a square, in the square inscribed is another circle and in
that circle another square and so on, as is shown in the figure
below. Find the sum of areas of all
the circles and the sum of areas of all the squares. |
| Solution:
It follows that
the radius r
is the half of the diagonal d
of the first inscribed square, |
|
|
|
|
|
| Example:
In an isosceles triangle with the base 2a
and the angle 2a,
opposite to the base, inscribed are infinite sequence of circles
such that first circle touches the base and opposite sides of the
triangle while other circles touch opposite sides of the triangle and
the preceding circle, as shows the figure below. Find the sum of
all circumferences and areas of all inscribed
circles. |
| Solution:
In the shown
right triangles we use following relations, |
|
|
 |
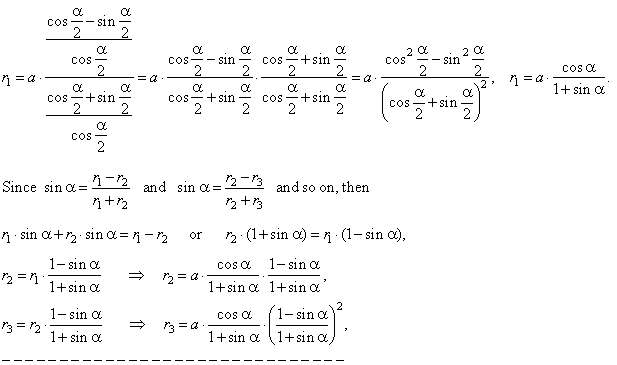| Therefore,
the sum of all circumferences, |
SC = 2pr1
+ 2pr2
+ 2pr3
+ . . . |
|
 |
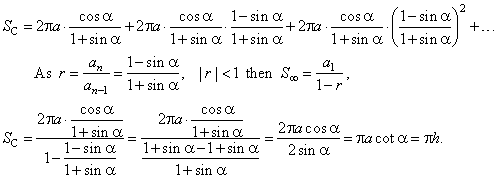| The sum of
areas of all circles, |
SA =
r12p
+ r22p
+ r32p
+ . . . |
|
 |
|
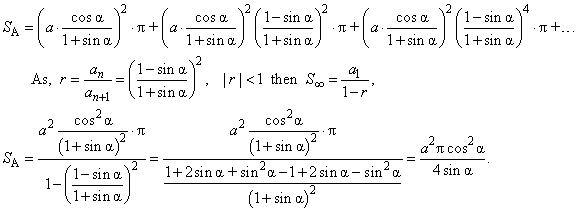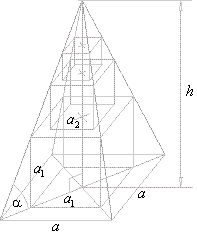
| Example:
Into the regular square pyramid, with the side of the base a
and the height h,
inserted is the square with the base lying in the base of the pyramid,
and the upper base of which is cross section of the pyramid. Into the
space above this square inserted is, the same way, another square, and
above of this third square and so on, to infinity, as is shown in the
figure below. Find the
volume of
all inserted squares. |
| Solution:
Following
relations hold between similar right triangles shown in the figure, |
 |
|
 |
|
 |
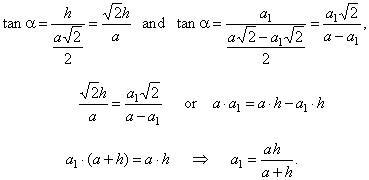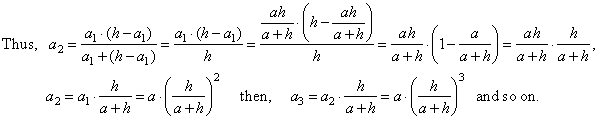| The sum of
volumes of all the squares, |
SV =
V1
+ V2
+ V3
+ . . . = a13
+ a23
+ a33
+ . . . |
|
 |
|
|
|
|
|
|
|
|
|
|
|
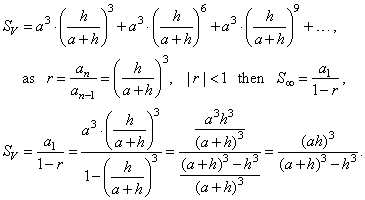| Intermediate
algebra contents |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
