|
|
|
|
Mathematical
Induction
|
|
Mathematical
induction examples
|
|
|
|
|
|
|
| Mathematical
Induction
|
| Mathematical
induction is a formal method of proving that all
positive integers n have a certain property P(n). |
| The principle of
mathematical induction states that a statement P(n) is
true for all positive integers, n Î N |
|
(i)
if
it is true for n
= 1, that
is, P(1)
is true
and |
|
(ii)
if
P(k) is
true implies P(k
+ 1) is
true. |
|
| Thus,
every proof using the mathematical induction consists of the following
three steps: |
|
1)
Prove that the statement is true for the first term in the sequence (or
series), |
|
i.e., prove P(1)
is true
for n
= 1, |
|
2)
Assume that the statement is true for a particular value
n
= k, |
|
i.e., assume P(k) is
true |
|
3)
Prove that the statement is true for the next term in the sequence n
= k
+ 1, |
|
i.e., prove P(k) is
true implies P(k
+ 1) is
true. |
|
| Mathematical
induction examples
|
| Example: Prove
by
mathematical induction that for all positive integers n
|
| 1
+ 3 + 5 + . . . + (2n -
1) = n2 |
| Solution:
1) For
n
= 1, we
have 2 · 1 -
1 = 12, therefore
P(1)
holds, |
|
2)
Assume that the statement is true for a particular value
n
= k, that is
|
| 1
+ 3 + 5 + . . . + (2k -
1) = k2 |
|
3) Prove that the sum is true for n
= k
+ 1, that is
|
| 1
+ 3 + 5 + . . . + [2(k + 1) -
1] = (k + 1)2 |
|
If, to the left and right side of the equality
2) we add 2k + 1
increased is given series by next term
|
|
1
+ 3 + 5 + . . . + (2k -
1) + 2k + 1 = k2
+ 2k + 1 = (k + 1)2
|
|
thus, the given statement is true
for all positive integers.
|
|
|
| Example: Prove
by
mathematical induction that for all positive integers n
|
| 1
+ 2 + 3 + . . . + n = n(n + 1)/2 |
| Solution:
1) For
n
= 1, we
have 1 = 1 ·
(1 + 1)/2 = 1, therefore
P(1)
holds, |
|
2)
Assume that the statement is true for a particular value
n
= k, that is
|
| 1
+ 2
+ 3 + . . . + k = k(k + 1)/2 |
|
3) Prove that the sum is true for n
= k
+ 1, that is
|
|
1
+ 2
+ 3 + . . . + (k + 1) = (k + 1)(k + 2)/2
|
|
If, to the left and right side of the equality
2) we add k + 1 increased is given series by next term
|
|
1
+ 2
+ 3 + . . . + k + (k + 1) = k(k + 1)/2
+ (k + 1) = [k(k + 1) + 2(k + 1)]/2
= (k + 1)(k + 2)/2
|
|
therefore, the given statement is true for all
positive integers.
|
|
|
| Example: Prove
by
mathematical induction that for all positive integers n
|
| 12
+ 22
+ 32 + . . . + n2 = n(n + 1)(2n + 1)/6 |
| Solution:
1) For
n
= 1, we
have 12
= 1 · ( 1 + 1)(2 · 1 + 1)/6 =
6/6 = 1 therefore
P(1)
holds, |
|
2)
Assume that the statement is true for a particular value
n
= k, that is
|
| 12
+ 22
+ 32 + . . . + k2 = k(k + 1)(2k + 1)/6 |
|
3) Prove that the sum is true for n
= k
+ 1, that is
|
| 12
+ 22
+ 32 + . . . + (k + 1)2 = (k + 1)(k +
2)(2k + 3)/6 |
|
If, to the left and right side of the equality
2) we add (k + 1)2
increased
is given series by next term
|
| 12
+ 22
+ 32 + . . . + k2 + (k + 1)2 =
k(k + 1)(2k + 1)/6 + (k + 1)2 = (k + 1)(2k2
+ 7k + 6)/6 |
|
= (k + 1)(k + 2)(2k + 3)/6
|
|
therefore, the given statement is true for all
positive integers.
|
|
|
| Example: Prove
by
mathematical induction that for all positive integers n
|
| 1 ·
2 + 2 · 3 + 3 · 4 + . . . + n · (n + 1) = n(n + 1)(n +
2)/3 |
| Solution:
1) For
n
= 1, we
have 1 · 2 = 1 ·
(1 + 1)(1 + 2)/3 = 1 · 2 therefore
P(1)
is
true, |
|
2)
Assume that the statement is true for a particular value
n
= k, that is
|
| 1 ·
2 + 2 · 3 + 3 · 4 + . . . + k · (k + 1) = k(k + 1)(k +
2)/3 |
|
3) By
adding (k + 1) ·
(k + 2) to
both sides of of the equality
2), that is
|
| 1 ·
2 + 2 · 3 + 3 · 4 + . . . + k · (k + 1) + (k + 1)
· (k + 2) = k(k + 1)(k +
2)/3 + (k + 1) · (k + 2) |
|
= (k + 1)(k + 2)(k + 3)/3
|
| given
sum is increased by the value of the next term of the series to prove
P(n
+ 1) is
true for all
positive integers.
|
|
|
| Example: Prove
by
mathematical induction that the formula an
= a1 + (n -
1)d, |
|
for
the general term of an arithmetic sequence,
holds.
|
|
Solution: 1) For
n
= 1, we obtain an
= a1 + (1 -
1)d = a1, so P(1)
is
true,
|
|
2)
Assume that the formula an
= a1 + (n -
1) holds
for all
positive integers n
> 1, then
|
|
3)
We should prove that the formula holds
for n + 1, that is
an
+ 1 = a1 + [(n + 1) -
1]d = a1 + n ·
d.
|
|
Since, by assumption an
= a1 + (n -
1)d, and by the
definition of an arithmetic sequence an
+ 1 -
an
= d,
|
|
then, an
+ 1 = an + d = a1
+ (n -
1)d + d = a1 + n ·
d.
|
|
|
| Example: Prove
by
mathematical induction that the formula Sn
= (n/2) ·
(a1 +
an) for
the sum of the first n
terms of an arithmetic sequence,
holds.
|
|
Solution: 1) For
n
= 1, we obtain S1
= (1/2) ·
(a1 +
a1)
= a1, so P(1)
is
true,
|
|
2)
Assume that the formula Sn
= (n/2) ·
(a1 +
an) holds
for all
positive integers n
> 1, then
|
|
3)
We should prove that the formula holds
for n + 1, that is |
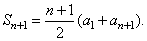 |
|
| Proof, since
|
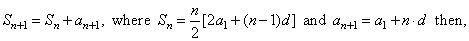 |
|
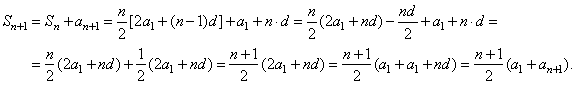
|
|
|
| Example: Prove
by
mathematical induction that the formula an
= a1 ·
r n
-
1 for
the general term of a geometric sequence,
holds.
|
|
Solution: 1) For
n
= 1, we obtain an
= a1 ·
r 1
-
1
= a1, so P(1)
is
true,
|
|
2)
Assume that the formula an
= a1 ·
r n
-
1 holds
for all
positive integers n
> 1, then
|
|
3)
We should prove that the formula holds
for n + 1, that is
an
+ 1 = a1 ·
r (n + 1)
-
1 = a1 ·
r n.
|
|
Since, by assumption an
= a1 ·
r n
-
1, and by the
definition of a geometric
sequence an
+ 1
= an ·
r,
|
|
then, an
+ 1 = an ·
r = a1 ·
r n
-
1 ·
r = a1 ·
r n.
|
|
|
| Example: Prove
by
mathematical induction that the formula |
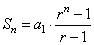 |
|
| for
the sum of the first n
terms of
a geometric sequence,
holds.
|
| Solution:
1) For
n
= 1, we obtain |
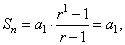 |
so P(1)
is
true,
|
|
| 2)
Assume that the formula |
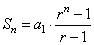 |
holds
for all
positive integers n
> 1, then
|
|
|
3)
We should prove that the formula holds
for n + 1, that is |
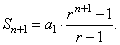 |
|
| Proof, as |
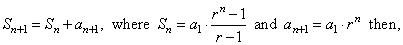 |
|
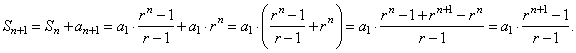
|