|
|
|
|
Quadratic Equations and Quadratic
Function |
 Quadratic function or
the second-degree polynomial
Quadratic function or
the second-degree polynomial |
|
Translated form of
quadratic function |
|
Vertex (maximum/minimum) - coordinates of translation
|
|
Roots or zeros of the
function, axis of symmetry and y-intercept |
 Graphing a quadratic
function
Graphing a quadratic
function |
|
Transformations
of the graph of the quadratic function |
|
|
|
|
|
|
| Quadratic function or
the second-degree polynomial |
| The
polynomial function of the second degree, f
(x)
=
a2x2
+ a1x
+ a0, is called a
quadratic function. |
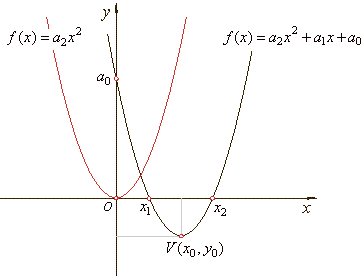 |
| |
y
= f (x)
=
a2x2
+ a1x
+ a0
or y
-
y0
= a2(x
-
x0)2, |
|
|
| where |
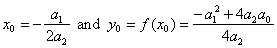 |
are the coordinates
of translations of the quadratic |
|
|
function. By
setting x0
= 0
and
y0
= 0 we obtain
y
=
a2x2,
the source quadratic function.
|
|
The turning point V
(x0,
y0)
is called the vertex of the parabola.
|
|
Note that the coefficients, a2, a1
and a0,
of quadratic function, correspond to the coefficients, a, b
and c,
of
|
|
quadratic equation, respectively.
|
| The
real zeros of the
quadratic function: |
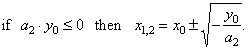 |
|
|
|
The above formula is known quadratic formula
that shows the
symmetry
of the roots relative to the axis of
|
|
symmetry of the
parabola.
|
| |
y
= f (x) =
a2x2
+ a1x
+ a0 = a2(x
- x1)(x
- x2)
= a2[x2
-
(x1 +
x2)x
+
x1x2] |
|
|
| The graph of a quadratic function is curve called a parabola. The parabola is symmetric with respect to a vertical line
called the axis of symmetry. |
| As
the axis of symmetry passes through the vertex of the parabola
its equation is x
= x0. |
| Quadratic
function has the y-intercept at the
point ( 0,
a0 ).
|
|
| Translated form of
quadratic function |
| The
proof that quadratic function f
(x)
= a2x2 + a1x
+ a0
is translation of its source or original
f (x)
= a2x2 |
| 1)
Let calculate the
coordinates of translations of quadratic function using the
formulas, |
| substitute
n
= 2 in |
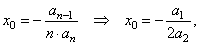 |
|
|
| then |
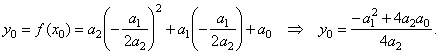 |
|
|
| 2)
To
get the source quadratic function we should plug the coordinates
of translations (with changed signs) |
|
into the general form
of the quadratic,
i.e., |
 |
| after
expanding and reducing obtained is |
|
y
=
a2x2
the source quadratic function |
| 3)
Inversely, by plugging the coordinates of translations into the source quadratic function |
|
y
-
y0
= a2(x
-
x0)2, |
|
|
| and
after
expanding and reducing we obtain |
|
y
=
a2x2
+ a1x
+ a0 the quadratic function
in the general form. |
|
| Graphing a quadratic
function |
| Transformations
of the graph of the quadratic function |
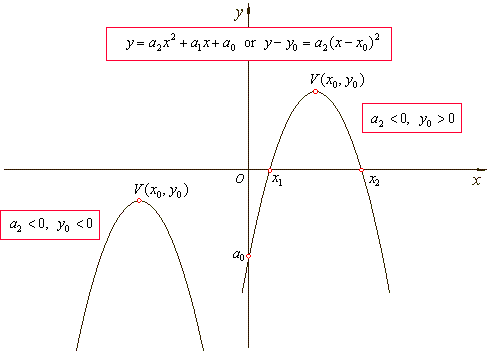
| How
changes in the expression of the quadratic function affect its
graph is shown in the figures below. |
|
|
|
|
 |
|
The graph of quadratic polynomial will intersect the
x-axis in two
distinct points if its leading coefficient a2 and the vertical translation
y0
have different signs, i.e., if a2
· y0
<
0. |
|
|
| Example:
Find zeros and vertex of
the quadratic function y
=
-
x2
+ 2x
+
3
and sketch its graph. |
| Solution:
A quadratic function can
be rewritten into translatable form y
-
y0
= a2(x
-
x0)2
by completing the square, |
|
y
=
-
x2
+ 2x
+ 3 |
Since a2
· y0
<
0 given
quadratic function must have two different real zeros. |
|
y
=
-
(x2
-
2x)
+ 3 |
To find zeros of a function, we set
y
equal to zero and solve for x.
Thus, |
|
y
=
-
[(x
-
1)2
-
1]
+ 3 |
-
4
=
-
(x
-
1)2 |
| y -
4
=
-
(x
-
1)2 |
(x
-
1)2
=
4 |
| y
-
y0
= a2(x
-
x0)2 |
x
-
1
=
±
sqrt(4) |
| V(x0,
y0)
=>
V(1,
4) |
x1,2
=
1
±
2, =>
x1
= -
1
and x2
= 3. |
|
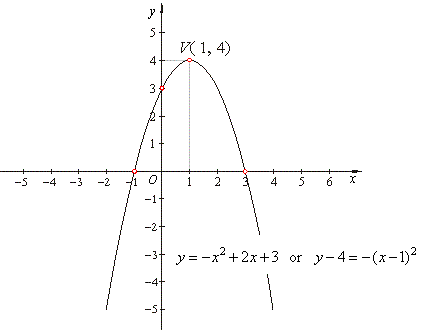 |
| We
can deal with the given quadratic using the property of the
polynomial explored under the title, |
| '
Source
or original polynomial function '. Thus, |
| 1)
calculate the coordinates of translations of the quadratic
y
=
f (x) =
-
x2
+ 2x
+
3 |
|
|
| 2)
To
get the source quadratic function, plug the coordinates
of translations (with changed signs) |
|
into the general form
of the quadratic, i.e., |
| y
+ y0
= a2(x
+ x0)2
+ a1(x
+ x0)
+ a0
=> y
+ 4
= -
(x
+ 1)2
+ 2(x
+ 1)
+
3 |
|
y
=
-
x2
the source quadratic function |
| 3)
Inversely, by plugging the coordinates of translations into the source quadratic function |
| y
- y0
= a2(x
- x0)2
=> y
- 4
= -
(x -
1)2
|
|
obtained is given quadratic in general form
y
=
-
x2
+ 2x
+
3. |
|
|
|
|
|
|
|
|
|
|
| Intermediate
algebra contents |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |