|
|
|
|
Quadratic Equations and Quadratic
Function |
 Quadratic equation
Quadratic equation |
|
Solving quadratic equations by completing the
square, the quadratic formula |
|
Solving quadratic equations by factoring, Vieta’s formula |
 Quadratic function or
the second-degree polynomial
Quadratic function or
the second-degree polynomial |
|
Translated form of
quadratic function |
|
Vertex (maximum/minimum) - coordinates of translation
|
|
Roots or zeros of the
function, axis of symmetry and y-intercept |
|
|
|
|
|
|
| Quadratic equation |
| A
quadratic equation is a polynomial equation of the second
degree. The general or standard form is |
| ax2
+ bx + c = 0,
a is
not 0 |
| where a,
b
and c
are coefficients. |
|
|
Solving quadratic equations by completing the
square, the quadratic formula |
| The solutions of the equation
are called roots (which may be real or complex) and are given by
the quadratic formula. |
|
We
use the completing the square method to derive the quadratic
formula to find the roots, |
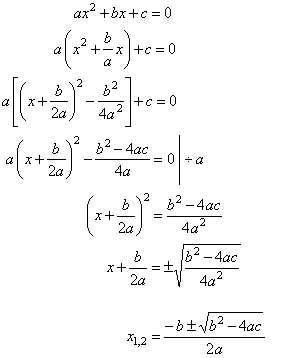 |
| The
roots can also be written |
 |
| If
c = 0,
the roots of the
equation ax2
+ bx = 0
we can obtain by factoring |
|
x(ax
+ b) = 0 |
| or
by using the quadratic formula, so we get x1=
0 and x2
= -b/a. |
|
| Solving quadratic equations by factoring, Vieta’s formula |
| A
quadratic trinomial ax2
+ bx
+ c
can be factorized as |
| ax2
+ bx
+ c
= a·[x2
+ (b/a)·x
+ c/a]
= a·(x
-
x1)(x
-
x2), |
where
x1
+ x2
= b/a and
x1·
x2
= c/a |
|
| That
means, to factor a quadratic trinomial we should find such a
pair of numbers x1
and x2
whose sum equals b/a
and whose product equals c/a. |
| So,
if a >
0 and the constant term c
negative, then the signs of x1
and x2
will be different while, when c
is positive, their signs will be the same. |
|
Then we use zero product principle to solve the quadratic equation,
that is, a product a
· b = 0
if at least one of its factors is 0. |
|
Examples:
Find the roots of each
quadratic equation by factoring:
|
|
a) x2
- 3x
-10
= 0
|
|
since
x2
- 3x
-10
= x2
+ (-5
+
2)·x
+ (-5)·(+2)
= x2
- 5x
+
2x
-10
|
|
= x ·
(x
- 5)
+ 2 ·
(x
- 5)
= (x
- 5)
·
(x
+ 2),
|
| then
x
- 5
= 0
=>
x1 =
5, or
x
+ 2
= 0
=>
x2 =
-2. |
|
| b) 2x2
- 7x
+ 3
= 0 |
|
as 2x2
- 7x
+ 3
= 2[x2
- (7/2)x
+ 3/2]
= 2[x2
- (1/2)x
- 3x
+ 3/2]
= |
|
= 2[x(x
- 1/2)
- 3(x - 1/2)]
= 2
(x - 1/2)(x
- 3)
= (2x
- 1)
(x - 3), |
| then
2x
- 1
= 0
=>
x1 =
1/2, or
x - 3
= 0
=>
x2 =
3 |
|
| c) 3x2
- x
- 2
= 0 |
|
as 3x2
- x
- 2
= 3[x2
- (1/3)x
- 2/3]
= 3[x2 +
(2/3)x
- x
- 2/3]
= |
|
= 3[x(x
+ 2/3)
-
(x + 2/3)]
= 3·(x
+ 2/3)(x
- 1)
= (3x + 2)(x
- 1), |
| then
3x + 2
= 0
=>
x1 =
-2/3, or
x
- 1
= 0
=>
x2 =
1. |
|
|
| Example:
Given
are leading
coefficient a2
=
-1
and
the pair
of conjugate complex
roots, |
|
x1 =
1 +
i
and
x2
=
1 - i,
of
a second
degree polynomial; |
| a)
find
the polynomial using
the above theorem, |
| b)
make a check of the solutions of the polynomial using the
quadratic formula. |
| Solution: |
a)
By
plugging the given values into a2x2
+ a1x
+ a0 = a2(x
- x1)
(x
- x2) |
|
a2x2
+ a1x
+ a0 = -1[x
-
(1
+ i)]
· [x
-
(1 - i)]
= -[(x
- 1)
- i]
· [(x - 1)
+ i]
=
|
|
= -[(x - 1)2
- i2]
=
-(x2
- 2x
+ 1 +
1)
=
- x2
+ 2x
- 2 |
|
b)
Check the polynomial for the roots, |
|
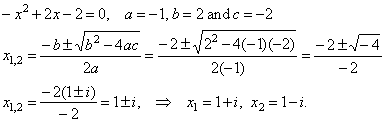 |
|
|
| Quadratic function or
the second-degree polynomial |
| The
polynomial function of the second degree, f
(x)
=
a2x2
+ a1x
+ a0, is called a
quadratic function. |
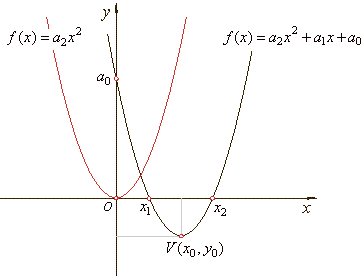 |
| |
y
= f (x)
=
a2x2
+ a1x
+ a0
or y
-
y0
= a2(x
-
x0)2, |
|
|
| where |
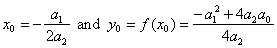 |
are the coordinates
of translations of the quadratic |
|
|
function. By
setting x0
= 0
and
y0
= 0 we obtain
y
=
a2x2,
the source quadratic function.
|
|
The turning point V(x0,
y0)
is called the vertex of the parabola.
|
|
Note that the coefficients, a2, a1
and a0,
of quadratic function, correspond to the coefficients, a, b
and c,
of
|
|
quadratic equation, respectively.
|
| The
real zeros of the
quadratic function: |
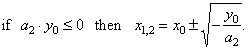 |
|
|
|
The above formula is known quadratic formula
that shows the
symmetry
of the roots relative to the axis of
|
|
symmetry of the
parabola.
|
| |
y
= f (x) =
a2x2
+ a1x
+ a0 = a2(x
- x1)(x
- x2)
= a2[x2
-
(x1 +
x2)x
+
x1x2] |
|
|
| The graph of a quadratic function is curve called a parabola. The parabola is symmetric with respect to a vertical line
called the axis of symmetry. |
| As
the axis of symmetry passes through the vertex of the parabola
its equation is x
= x0. |
| Quadratic
function has the y-intercept at the
point ( 0,
a0 ).
|
|
| Translated form of
quadratic function |
| The
proof that quadratic function f
(x)
= a2x2 + a1x
+ a0
is translation of its source or original
f (x)
= a2x2 |
| 1)
Let calculate the
coordinates of translations of quadratic function using the
formulas, |
| substitute
n
= 2 in |
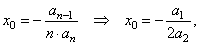 |
|
|
| then |
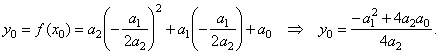 |
|
|
| 2)
To
get the source quadratic function we should plug the coordinates
of translations (with changed signs) |
|
into the general form
of the quadratic,
i.e., |
 |
| after
expanding and reducing obtained is |
|
y
=
a2x2
the source quadratic function |
| 3)
Inversely, by plugging the coordinates of translations into the source quadratic function |
|
y
-
y0
= a2(x
-
x0)2, |
|
|
| and
after
expanding and reducing we obtain |
|
y
=
a2x2
+ a1x
+ a0 the quadratic function
in the general form. |
|
|
|
|
|
|
|
|
|
|
| Intermediate
algebra contents |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |