|
|
|
| Interest
Calculations |
 Exponential
growth and decay, application of the natural exponential
function
Exponential
growth and decay, application of the natural exponential
function |
|
|
|
|
|
|
| Exponential
growth and decay, application of the natural exponential
function |
| We
use the same formula as for continuous compound interest in many natural processes
where the rate of change of a
quantity through time is proportional to the current amount of the quantity,
represented by the differential equation |
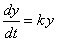 |
|
where, y
is a function of time t,
whose value y(0)
= y0 at
t
= 0, and k
is a constant. |
| We solve
the given differential equation
with initial condition y(0)
= y0 to find y
as function of t,
by separating the variables |
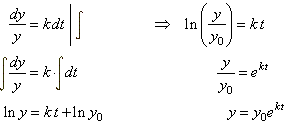 |
|
| A
quantity is said to be subject to exponential growth if it
increases at a rate proportional to its current value. |
| The
constant k
is called the growth rate and in
exponential growth k
> 0. The rate constant k
depends only on the process and the conditions under which it is
carried out. |
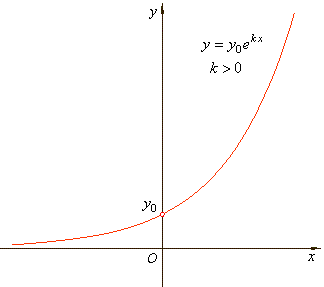 |
|
| A
quantity is said to be subject to exponential decay if it
decreases at a rate proportional to its current value. |
| The
constant k
is called the decay
rate and in exponential decay k
< 0. |
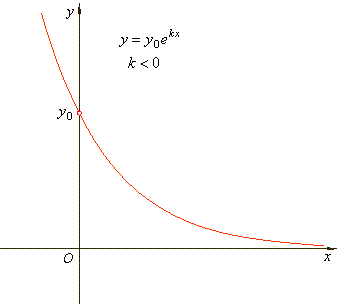 |
|
|
| Example:
Suppose that
microorganisms in a culture dish grow exponentially. At the
start of an experiment there are 8,000 of bacteria, and two
hours later the population has increased to 8,600. How long will
it take for the population to reach 20,000? |
| Solution: Given the initial
population N0
= 8,000 and for t
=
2 hours
the population increased to N
= 8,600. |
| We
first find the growth rate k
and then the time needed the population increases to 20,000. |
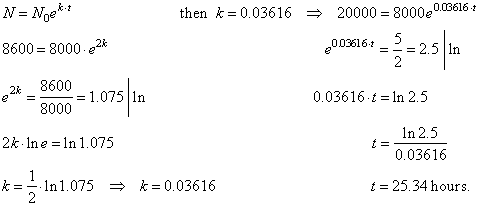 |
|
| Radioactive decay is a
typical example to which the exponential decay model can be
applied. |
| Example:
After 800
years a sample of radioisotope radium-226 has decayed to 70.71%
of its initial mass, find the half-life of radium-226. |
| Solution:
The half-life of a radioactive material is the amount of time
required for half of a given sample to |
| decay.
First
we plug the given information into the formula for exponential
decay |
|
N(t)
= N0 ekt to
find the decay constant k. |
| Since
N0
is the initial quantity, N(t)
is the quantity after time t
and k
is the decay constant then, |
| by
substituting
N(t = 800) = 0.7071·N0
into
the formula |
| 0.7071N0
= N0 e k ·
800 |
| and
solving for k,
0.7071 =
e k · 800
| ln |
|
ln 0.7071 = 800 · k |
|
k = ln (0.7071) / 800 |
|
k = -
0.0004332217. |
| Thus,
the formula for the amount of radium-226 present at a time t
is |
| N(t)
= N0 e -
0.0004332217 · t |
| As
we want determine the half-life or the time for half of a substance to decay,
we substitute N(t)
= (1/2) N0 |
| into
the formula |
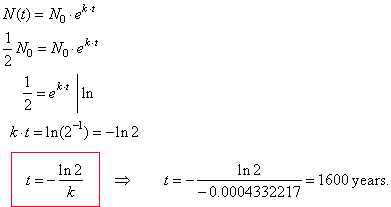 |
|
|
|
|
|
|
|
|
|
|
| Intermediate
algebra contents |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |