Interest calculations, Compound interest - periodic and continuous compounding

Interest Calculations

Compound interest

In compound interest calculations, the interest earned in each period is added at the end of a period to the principal of the previous period, to become the principal for the next period.

The compounding periods can be yearly, semiannually, quarterly, or the interest can be compounded more frequently even continuously.

Thus, if P is the principal or initial value of investment and the compound interest rate is i %, then

I₁ = i P is the amount of interest earned in the first period.

So, at the end of the first period, the accumulated amount is

A₁ = P + I₁ = P + i P = P(1 + i).

Since the accumulated amount at the end of the first period serve as the principal amount at the beginning of the second period, then the amount of interest earned in the second period is

I₂ = i A₁ = i P(1 + i)

therefore the accumulated amount at the end of the second period is

A₂ = A₁ + I₂ = P(1 + i) + i P(1 + i) = P(1 + i)(1 + i) = P(1 + i)².

Thus, at the end of n periods (or after n years) the accumulated amount or final value of investment is

A_n = A = P(1 + i)(1 + i) · · · (1 + i) = P(1 + i)ⁿ

A_n = A = P · r ⁿ, where r = 1 + i

therefore,

Example: If $10,000 is invested for five years at 6% of the interest rate, find the accumulated or final value and total interest earned at the end of the period under both, simple and compound interest.

Solution: a) Under simple interest,

the total interest earned in five years period is

I = i% · P · n => I = 6/100 · 10000 · 5 = $3000,

the accumulated value after five years period is

A = P + I = P (1 + i n) => A = 10000 · (1 + 6/100 · 5) = 10000 · 1.3 = $13000,

so that I = A - P = 13000 - 10000 = $3000.

b) Under compound interest,

the accumulated value after five years period is

A = P(1 + i%)ⁿ => A = 10000 · (1 + 0.06)⁵ = 10000 · 1.338225 = $13382.25

therefore, the total interest earned in five years period is

I = A - P = 13382.25 - 10000 = $3382.25.

So, the interest compounding (or interest earned on interest) brings the extra $382.25 in comparison with the simple interest.

Example: After how many years will deposit double at an interest rate of 6%.

Solution:

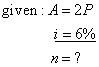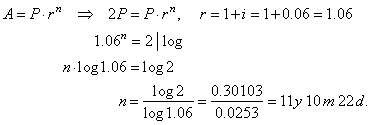Example: At what annual interest has to be deposited $5,000 for four years to grow to $8,000.

Solution:

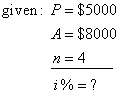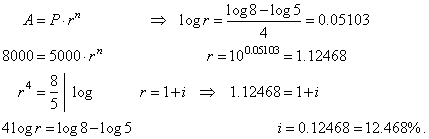Periodic compounding

Note that for any given interest rate the investment grows more if the compounding period is shorter.

So, if P is an amount of money invested for n years at an interest rate i, compounded m times per year, then the total number of compounded periods is mn and the interest rate per period is i/m and the accumulated or future value is

Example: The principal amount of $2,000 is invested for five years in a compound interest account paying 6% compounded quarterly, find the final or accumulated amount in the account.

Solution:

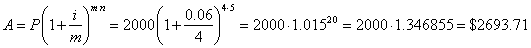Continuous compounding

As for any given interest rate the investment grows more if the compounding period is shorter, we let the number of periods in a year approach infinity to compound the interest continuously, meaning that the balance grows by a small amount every instant.

Thus, to derive a formula for continuous compounding we need to evaluate the above formula when m tends to infinity (i.e., the year is divided into infinite number of periods)

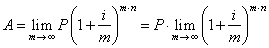then by substituting

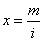and, when m ® oo then x ® oo,

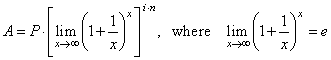that is, the limit in the square brackets converges to the number e = 2.71828 . . . , the base of natural logarithms, thus obtained is

the continuous compounding formula.

If in the above formula we write the final value of balance as function of time t (with t measured in years)

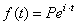and take its derivative at t,

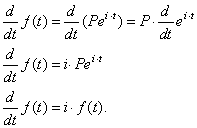The result shows that at any instant the balance is changing at a rate that equals i times the current balance which correspond to the definition of continuous compounding.

Example: Suppose $5,000 is deposited into an account that pays interest compounded continuously at an annual rate of 8%. How much will the account be worth in 20 years?

Solution:

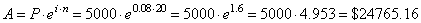Intermediate algebra contents