Interest calculations, Simple interest

Interest Calculations

Simple interest

Amount of interest, principal (initial amount), interest rate and amount after n years

Compound interest

Periodic compounding

Continuous compounding

Simple interest

An amount of money deposited into a bank for a given period of time brings to the depositor a profit called interest.

The amount of interest ( I ) the bank pays you, depends on the interest rate ( i % ), the amount of money deposited, denoted as principal P also called original balance (or initial investment), and the period of time n the money is deposited,

since P : 1 = I : (i · n) =>

Therefore,

Simple interest is calculated on a yearly basis (annually, n = 1) in which balance grows linearly with time (as opposed to compound interest).

That is, the interest stays unchanged in each next year of saving because it is always calculated as the percent of the same value, i.e., of the original principal P, while in the compound interest it is calculated as the percent of the sum of the balance and the interest from the previous period.

If P is the principal (or initial value of investment) and I is the interest amount, the accumulated value A (or final value of investment) at the end of n investment periods is given by

A = P + I = P + i · P · n = P (1 + i n).

and

Example: Somebody deposits $20,000 into a savings account where the rate of interest is 4.8% annually.

How much money in interest will earn after nine months?

Solution:

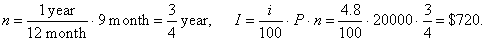Example: A bank lends a company money for the six months period at a rate of 8% annually.

How much was lent if the company should pay $12,000 of interest?

Solution:

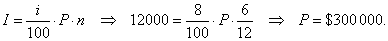Example: At what an interest rate was borrowed $75,000 for one year if $3,000 to interest is charged?

Solution:

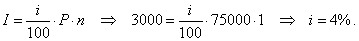Example: For what period of time should be deposited $200,000 at a 6% interest rate to earn $6,000 of

interest?

Solution:

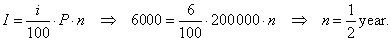Compound interest

In compound interest calculations, the interest earned in each period is added at the end of a period to the principal of the previous period, to become the principal for the next period.

The compounding periods can be yearly, semiannually, quarterly, or the interest can be compounded more frequently even continuously.

Thus, if P is the principal or initial value of investment and the compound interest rate is i %, then

I₁ = i P is the amount of interest earned in the first period.

So, at the end of the first period, the accumulated amount is

A₁ = P + I₁ = P + i P = P(1 + i).

Since the accumulated amount at the end of the first period serve as the principal amount at the beginning of the second period, then the amount of interest earned in the second period is

I₂ = i A₁ = i P(1 + i)

therefore the accumulated amount at the end of the second period is

A₂ = A₁ + I₂ = P(1 + i) + i P(1 + i) = P(1 + i)(1 + i) = P(1 + i)².

Thus, at the end of n periods (or after n years) the accumulated amount or final value of investment is

A_n = A = P(1 + i)(1 + i) · · · (1 + i) = P(1 + i)ⁿ

A_n = A = P · r ⁿ, where r = 1 + i

therefore,

Example: If $10,000 is invested for five years at 6% of the interest rate, find the accumulated or final value and total interest earned at the end of the period under both, simple and compound interest.

Solution: a) Under simple interest,

the total interest earned in five years period is

I = i% · P · n => I = 6/100 · 10000 · 5 = $3000,

the accumulated value after five years period is

A = P + I = P (1 + i n) => A = 10000 · (1 + 6/100 · 5) = 10000 · 1.3 = $13000,

so that I = A - P = 13000 - 10000 = $3000.

b) Under compound interest,

the accumulated value after five years period is

A = P(1 + i%)ⁿ => A = 10000 · (1 + 0.06)⁵ = 10000 · 1.338225 = $13382.25

therefore, the total interest earned in five years period is

I = A - P = 13382.25 - 10000 = $3382.25.

So, the interest compounding (or interest earned on interest) brings the extra $382.25 in comparison with the simple interest.

Example: After how many years will deposit double at an interest rate of 6%.

Solution:

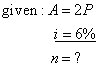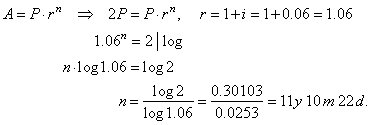Example: At what annual interest has to be deposited $5,000 for four years to grow to $8,000.

Solution:

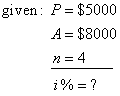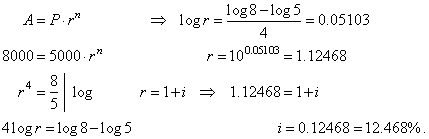Periodic compounding

Note that for any given interest rate the investment grows more if the compounding period is shorter.

So, if P is an amount of money invested for n years at an interest rate i, compounded m times per year, then the total number of compounded periods is mn and the interest rate per period is i/m and the accumulated or future value is

Example: The principal amount of $2,000 is invested for five years in a compound interest account paying 6% compounded quarterly, find the final or accumulated amount in the account.

Solution:

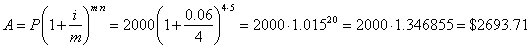Continuous compounding

As for any given interest rate the investment grows more if the compounding period is shorter, we let the number of periods in a year approach infinity to compound the interest continuously, meaning that the balance grows by a small amount every instant.

Thus, to derive a formula for continuous compounding we need to evaluate the above formula when m tends to infinity (i.e., the year is divided into infinite number of periods)

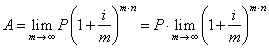then by substituting

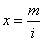and, when m ® oo then x ® oo,

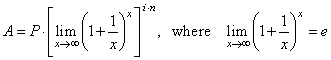that is, the limit in the square brackets converges to the number e = 2.71828 . . . , the base of natural logarithms, thus obtained is

the continuous compounding formula.

If in the above formula we write the final value of balance as function of time t (with t measured in years)

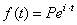and take its derivative at t,

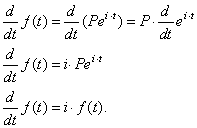The result shows that at any instant the balance is changing at a rate that equals i times the current balance which correspond to the definition of continuous compounding.

Example: Suppose $5,000 is deposited into an account that pays interest compounded continuously at an annual rate of 8%. How much will the account be worth in 20 years?

Solution:

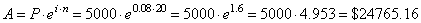Intermediate algebra contents