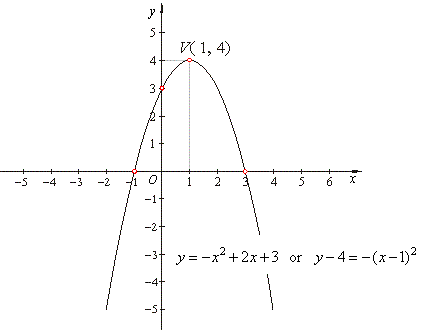Quadratic Equations and Quadratic Function
      Graphing a quadratic function
         Transformations of the graph of the quadratic function
 
    Quadratic Inequalities
      Solving quadratic inequality graphically
Graphing a quadratic function
Transformations of the graph of the quadratic function
How changes in the expression of the quadratic function affect its graph is shown in the figures below.
    The graph of quadratic polynomial will intersect the x-axis in two distinct points if its leading coefficient   a2  and the vertical translation y0 have different signs, i.e., if   a2 · y0 < 0. 
Example:  Find zeros and vertex of the quadratic function  y = - x2 + 2x + 3  and sketch its graph.
Solution:  A quadratic function can be rewritten into translatable form  y - y0 = a2(x - x0)2  by completing the square,
      y = - x2 + 2x + 3    Since a2 · y0 < 0 given quadratic function must have two different real zeros.
      y = - (x2 - 2x) + 3   To find zeros of a function, we set y equal to zero and solve for x. Thus,
      y = - [(x - 1)2 - 1] + 3                         - 4 = - (x - 1)2
y - 4 = - (x - 1)2                  (x - 1)2 = 4
y - y0 = a2(x - x0)2                      x - 1 = ± sqrt(4)
V(x0, y0)  =>   V(1, 4)                        x1,2 = 1 ± 2,   =>    x1 = - 1 and  x2 = 3.
We can deal with the given quadratic using the property of the polynomial explored under the title,
' Source or original polynomial function '. Thus,
1)  calculate the coordinates of translations of the quadratic  y = f (x) = - x2 + 2x + 3
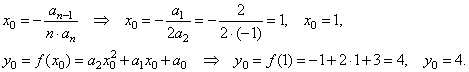
2)  To get the source quadratic function, plug the coordinates of translations (with changed signs)
     into the general form of the quadratic, i.e.,
y + y0 = a2(x + x0)2 + a1(x + x0) + a0   =>    y + 4 = - (x + 1)2 + 2(x + 1) + 3
                                                                                              y = - x2   the source quadratic function
3)  Inversely, by plugging the coordinates of translations into the source quadratic function
y - y0 = a2(x - x0)2   =>     y - 4 = - (x - 1)2
                    obtained is given quadratic in general form     y = - x2 + 2x + 3.
Quadratic Inequalities
To solve a quadratic inequality we can examine the sign of the equivalent quadratic function.
The x-intercepts or roots are the points where a quadratic function changes the sign. The x-intercepts determine the three intervals on the x-axis in which the function is above or under the x-axis, that is, where the function is positive or negative.
Example:   Solve the inequality  - x2 + 2x + 3 ≤ 0.
Solution:  Solve the quadratic equation  ax2 + bx + c = 0 to get the boundary points.
The zeroes or roots of equivalent function (see the graph below) are the endpoints of the intervals and are included in the solution.
The turning point V(x0, y0),
 
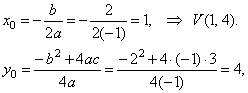The roots,  - x2 + 2x + 3 = 0
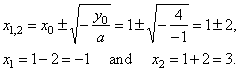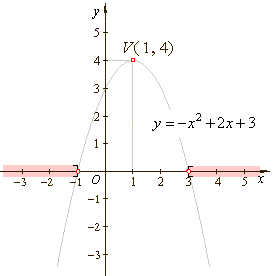Solution:  
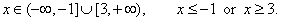Intermediate algebra contents
Copyright © 2004 - 2020, Nabla Ltd.  All rights reserved.