|
| Combinatorics -
Combinatorial
Analysis |
|
|
|
|
Permutations
|
Permutations
|
|
Permutations
of n objects some of which are the
same |
|
|
|
|
|
|
| Permutations
|
| Given
a set of n
different elements or objects. Any distinct ordered arrangement of the n
elements is called permutation. |
| The total
number of permutations for n
elements is |
|
|
|
| Example:
Given is the sequence of four digits 1, 2, 3, 4.
Write all possible ordered arrangements or permutations of the 4
digits. |
|
Solution:
The number of
permutations of the given 4 digits, P(4)
= 4! = 4 · 3 · 2 · 1 = 24.
|
| The
permutations are, |
|
1, 2, 3, 4
2, 1, 3, 4
3, 1, 2, 4
4, 1, 2, 3 |
|
1, 2, 4, 3
2, 1, 4, 3
3, 1, 4, 2
4, 1, 3, 2 |
|
1, 3, 2, 4
2, 3, 1, 4
3, 2, 1, 4
4, 2, 1, 3 |
|
1, 3, 4, 2
2, 3, 4, 1
3, 2, 4, 1
4, 2, 3, 1 |
|
1, 4, 2, 3
2, 4, 1, 3
3, 4, 1, 2
4, 3, 1, 2 |
|
1, 4, 3, 2
2, 4, 3, 1
3, 4, 2, 1
4, 3, 2, 1. |
|
|
| Permutations
of n objects some of which are the
same |
|
The number of
permutations of n
elements some groups of which are the same
|
|
|
| where,
k1,
k2,
. . . , km
denotes each group with identical elements. |
|
| Example:
How many different
7-letter words can be formed from the word GREETER? |
|
Solution:
|
 |
|
|
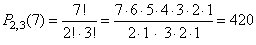| since
the letter R repeats twice and E repeats 3 times. |
|
| Example:
How many four-digit
numbers can be written with all of the digits 2, 3, 3, 4 and
write them in increasing order. |
|
Solution: In
the given sequence of four digits, the digit 3 repeat twice, so |
 |
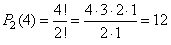| the
12 four-digit
numbers written in increasing
order are, |
|
2 3 3 4 3
2 3 4
4 2 3 3 |
|
2 3 4 3 3
2 4 3 4
3 2 3 |
|
2 4 3 3 3
3 2 4 4
3 3 2. |
|
3
3 4 2 |
|
3
4 2 3 |
|
3
4 3 2 |
|
|
|
|
|
|
|
|
|
|
| Intermediate
algebra contents |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
|
|
