|
|
|
|
The Binomial Theorem
|
Factorial
|
|
Binomial coefficients
|
|
The binomial theorem, sigma notation
and binomial expansion
algorithm |
|
The
binomial theorem and binomial expansion algorithm examples |
|
|
|
|
|
|
|
|
The Binomial Theorem
|
|
Factorial
|
| The
factorial is defined for a positive integer n,
denoted n!
represents the product of all positive integers less than or equal to n, |
|
n! = n · (n -
1) · · · 2 · 1. |
|
The first few factorials are, 1!
= 1, 2!
= 2 · 1
= 2, 3!
= 3 · 2 · 1 =
6, 4!
= 4 · 3
· 2 · 1
= 24, and so on.
|
|
By the definition, 0!
= 1. |
| So
for
example, n!
shows the number of ordered arrangements or permutations of n
objects, that is, on how many ways n
distinct objects can be arranged in a row. |
| Thus,
for example four digits 1, 2, 3, 4 can be arranged in 4!
= 24 ways, as is shown below |
|
1, 2, 3, 4
2, 1, 3, 4
3, 1, 2, 4
4, 1, 2, 3 |
|
1, 2, 4, 3
2, 1, 4, 3
3, 1, 4, 2
4, 1, 3, 2 |
|
1, 3, 2, 4
2, 3, 1, 4
3, 2, 1, 4
4, 2, 1, 3 |
|
1, 3, 4, 2
2, 3, 4, 1
3, 2, 4, 1
4, 2, 3, 1 |
|
1, 4, 2, 3
2, 4, 1, 3
3, 4, 1, 2
4, 3, 1, 2 |
|
1, 4, 3, 2
2, 4, 3, 1
3, 4, 2, 1
4, 3, 2, 1 |
|
| Binomial coefficients
|
| A
binomial coefficient is a numerical factor that multiply the successive
terms in the expansion of the binomial (a
+ b)n,
for integral n,
written |
 |
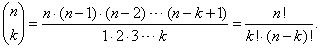| So
that, the general term, or the (k
+ 1)th
term, in the expansion of (a
+ b)n, |
 |
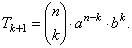| For
example, |
 |
|
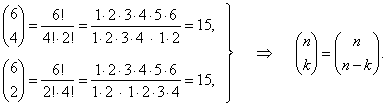| A
binomial coefficient equals the number of ways that r
objects can be selected from n
objects without regard to order, called combinations and noted C(n,
r) or Cnr. |
| For
example, the number of distinct combinations of three digits selected from
1, 2, 3, 4, 5 is |
 |
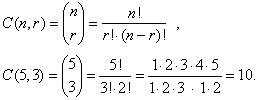| 1
2 3 2
3 4 3
4 5 |
| 1
2 4 2
3 5 |
| 1
2 5 2
4 5 |
| 1
3 4 |
| 1
3 5 |
| 1
4 5 |
|
|
|
|
The binomial theorem, sigma notation
and binomial expansion
algorithm |
| The
theorem that shows the form of the expansion of any positive integral
power of a binomial (a
+ b)n
to a polynomial with n
+ 1 terms, |
 |
|
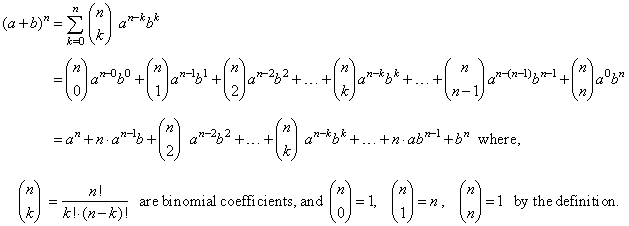| Example: Find
the middle
term of the binomial
expansion |
 |
|
|
|
|
| Example: Find
the 7th term of the binomial
expansion |
 |
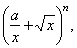if the coefficient of the third
term |
|
| relates
to the coefficient of the second term as 9 : 2. |
|
|
|
| Example:
Which term of the binomial
expansion |
 |
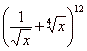is missing x? |
|
|
|
| To
fulfill the required condition, the exponent of x
must be zero, therefore |
 |
|
|
|
|
|
|
|
|
|
|
| Intermediate
algebra contents |
|
 |
|
| Copyright
© 2004 - 2020, Nabla Ltd. All rights reserved. |
|
|
