Combinatorial analysis - Combinations, combinations with repetition

Combinatorics - Combinatorial Analysis

Combinations

Combinations

Given a set of n different elements or objects. Select a subset of r elements out of n. Such selection is called the combination.

A combination is an unordered arrangement of r objects selected from n different objects taken r at a time.

The number of distinct combinations selecting r elements out of n is

Therefore, combinations must differ from each other at least in one element.

Example: Find the number of combinations of size 3 that can be made from digits 1, 2, 3, 4, 5 and write them out.

Solution: Since, n = 5 and r = 3 then

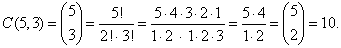The combinations are, 1 2 3 2 3 4 3 4 5.

1 2 4 2 3 5

1 2 5 2 4 5

1 3 4

1 3 5

1 4 5

Example: Find the number of combinations of size 4 that can be made from letters A, B, C, D, E, F and write them out.

Solution: Since, n = 6 and r = 4 then

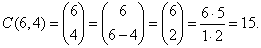The combinations are, A B C D B C D E C D E F.

A B C E B C D F

A B C F B C E F

A B D E B D E F

A B D F

A B E F

A C D E

A C D F

A C E F

A D E F

Combinations with repetition

The number of ways to choose r objects from a set of n different objects, so that an object can be chosen more than once

Remember that combinations must differ from each other at least in one element.

Example: Find the number of combinations of size 3 that can be made from digits 1, 2, 3, 4 if repetition is allowed, and write them out.

Solution: Since, n = 4 and r = 3 then

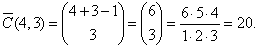The combinations are, 1 1 1 2 2 2 3 3 3 4 4 4 1 2 3

1 1 2 2 2 1 3 3 1 4 4 1 1 2 4

1 1 3 2 2 3 3 3 2 4 4 2 1 3 4

1 1 4 2 2 4 3 3 4 4 4 3 2 3 4

Example: Find the number of combinations of size 4 that can be made from letters A, B, C if repetition is allowed, and write them out.

Solution: Since, n = 3 and r = 4 then

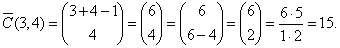The combinations with repetition are, A A A A B B B B C C C C A A B C

A A A B B B B C C C C A B B A C

A A B B B B C C C C A A C C A B.

A B B B B C C C C A A A

Intermediate algebra contents